题目内容
15．
如图，点D在△ABC的边AC上，若CD=2，AC=6，且△CDB∽△CBA，则BC2=12．
分析 由△CDB∽△CBA，根据相似三角形的对应边成比例，即可得CD：CB=CB：CA，继而求得答案．
解答 解：∵△CDB∽△CBA，
∴CD：CB=CB：CA，
∴BC2=CD•CA=2×6=12．
故答案为：12．
点评 此题考查了相似三角形的性质．注意相似三角形的对应边成比例．
练习册系列答案
相关题目
6．$\sqrt{4}$的算术平方根是（ ）
| A． | 4 | B． | 2 | C． | $\sqrt{2}$ | D． | ±2 |
3．
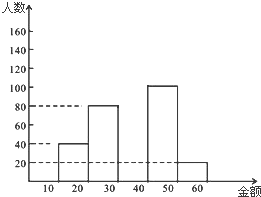四川雅安地震发生后，某校开展了为灾区捐款的活动．小明把本年级同学的捐款情况统计并制成图表，如图：
请根据图表提供的信息解答下列问题：
（1）表中m和n所表示的数分别是多少？M=160，n0.25．
（2）补全频数分布直方图；
（3）该校共有学生3000人，试估计全校为灾区捐款40元以上（包含40元）的学生人数．
四川雅安地震发生后，某校开展了为灾区捐款的活动．小明把本年级同学的捐款情况统计并制成图表，如图：| 金额（元） | 人数 | 频率 |
| 10≤x＜20 | 40 | 0.1 |
| 20≤x＜30 | 80 | 0.2 |
| 30≤x＜40 | m | 0.4 |
| 40≤x＜50 | 100 | n |
| 50≤x＜60 | 20 | 0.05 |
（1）表中m和n所表示的数分别是多少？M=160，n0.25．
（2）补全频数分布直方图；
（3）该校共有学生3000人，试估计全校为灾区捐款40元以上（包含40元）的学生人数．
20．直棱柱的侧面都是（ ）
| A． | 三角形 | B． | 长方形 | C． | 圆 | D． | 正方形 |
5．
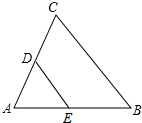如图，在△ABC中，D、E分别是边AC、AB上的点，下列命题中，假命题是（ ）
如图，在△ABC中，D、E分别是边AC、AB上的点，下列命题中，假命题是（ ）| A． | 若$\frac{AD}{AC}$=$\frac{DE}{BC}$，则△ADE与△ABC相似 | B． | 若$\frac{AD}{DC}$=$\frac{AE}{EB}$，则△ADE与△ABC相似 | ||
| C． | 若$\frac{AD}{AB}$=$\frac{AE}{AC}$，则△ADE与△ABC相似 | D． | 若∠ADE=∠B，则△ADE与△ABC相似 |