题目内容
把标准纸一次又一次对开,可以得到均相似的“开纸”.现在我们在长为2
、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是 .
| 2 |
考点:相似多边形的性质
专题:压轴题
分析:根据相似多边形对应边的比相等的性质分别求出所剪得的两个小矩形纸片的长与宽,进而求解即可.
解答:解:∵在长为2
、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,
∴要使所剪得的两个小矩形纸片周长之和最大,则这两个小矩形纸片长与宽的和最大.
∵矩形的长与宽之比为2
:1,
∴剪得的两个小矩形中,一个矩形的长为1,宽为
=
,
∴另外一个矩形的长为2
-
=
,宽为
=
,
∴所剪得的两个小矩形纸片周长之和的最大值是2(1+
+
+
)=4
+
.
故答案为:4
+
.
| 2 |
∴要使所剪得的两个小矩形纸片周长之和最大,则这两个小矩形纸片长与宽的和最大.
∵矩形的长与宽之比为2
| 2 |
∴剪得的两个小矩形中,一个矩形的长为1,宽为
| 1×1 | ||
2
|
| ||
| 4 |
∴另外一个矩形的长为2
| 2 |
| ||
| 4 |
7
| ||
| 4 |
| ||||
2
|
| 7 |
| 8 |
∴所剪得的两个小矩形纸片周长之和的最大值是2(1+
| ||
| 4 |
7
| ||
| 4 |
| 7 |
| 8 |
| 2 |
| 15 |
| 4 |
故答案为:4
| 2 |
| 15 |
| 4 |
点评:本题考查了相似多边形的性质,分别求出所剪得的两个小矩形纸片的长与宽是解题的关键.

练习册系列答案
相关题目
比较三个数-3,-π,-
的大小,下列结论正确的是( )
| 10 |
A、-π>-3>-
| ||
B、-
| ||
C、-
| ||
D、-3>-π>-
|
 在平面直角坐标系xOy中,点A在第一象限,点B(30,0),OA=
在平面直角坐标系xOy中,点A在第一象限,点B(30,0),OA= 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,
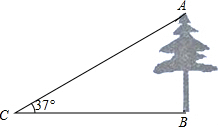 如图,在一次数学课外实践活动,小文在点C处测得树的顶端A的仰角为37°,BC=20m,求树的高度AB.
如图,在一次数学课外实践活动,小文在点C处测得树的顶端A的仰角为37°,BC=20m,求树的高度AB.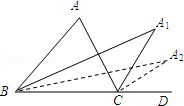 如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空:
如图,在△ABC中,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;…∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014,根据题意填空: