题目内容
18.(1)计算题:①-1$\frac{2}{3}$×(0.5-$\frac{2}{3}$)÷(-1$\frac{1}{9}$)
②-22-$\frac{1}{3}$×[(-5)2×(-$\frac{3}{5}$)-80÷(-4)×$\frac{1}{4}$]
(2)化简:2(2a2-9b)-3(-4a2+b)
分析 根据有理数运算法则以及整式运算法则即可求出答案.
解答 解:(1)①原式=-$\frac{5}{3}$×($\frac{1}{2}$-$\frac{2}{3}$)÷(-$\frac{10}{9}$)=-$\frac{1}{4}$;
②原式=-4-$\frac{1}{3}$×(-25×$\frac{3}{5}$+80×$\frac{1}{4}$×$\frac{1}{4}$)=-$\frac{2}{3}$;
(2)原式=4a2-18b+12a2-3b=16a2-21b
点评 本题考查有理数运算以及整式运算,属于基础题型,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.$\frac{8}{9}$的相反数是( )
| A. | $\frac{9}{8}$ | B. | $\frac{8}{9}$ | C. | -$\frac{8}{9}$ | D. | -$\frac{9}{8}$ |
9.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{{x}^{2}+1}{2}$,$\frac{3xy}{π}$,$\frac{3}{x+y}$,a+$\frac{1}{m}$,0中,分式的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.已知直线y1=k1x+b1(k1>0)与直线y2=k2x+b2(k2<0)的交点坐标为(2,-3),要使y1>y2成立,则下列选项中正确的是( )
| A. | x>2 | B. | x>-3 | C. | x<2 | D. | x<-3 |
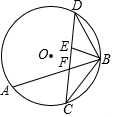 如图所示,在⊙O中,AB是一非直径的弦,点C是弧AB的中点,弦CD与AB交于点F,连结BD,作BE平分∠FBD交CD于点E.
如图所示,在⊙O中,AB是一非直径的弦,点C是弧AB的中点,弦CD与AB交于点F,连结BD,作BE平分∠FBD交CD于点E.