题目内容
12.化简求值:$\frac{a-2}{a+3}$÷$\frac{{a}^{2}-4}{2a+6}$-$\frac{5}{a+2}$,其中a=tan60°-$\frac{1}{sin30°}$.分析 先算除法,再算减法,最后求出a的值代入进行计算即可.
解答 解:原式=$\frac{a-2}{a+3}$•$\frac{2(a+3)}{(a+2)(a-2)}$-$\frac{5}{a+2}$
=$\frac{2}{a+2}$-$\frac{5}{a+2}$
=-$\frac{3}{a+2}$,
当a=$\sqrt{3}$-2时,原式=-$\frac{3}{\sqrt{3}}$=-$\sqrt{3}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
相关题目
20.下列各数中,最小的数是( )
| A. | -$\sqrt{5}$ | B. | -(-3) | C. | |-2| | D. | -π |
17.若4a2-kab+9b2是完全平方式,则常数k的值为( )
| A. | 6 | B. | 12 | C. | ±12 | D. | ±6 |
 如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
如图,将?ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.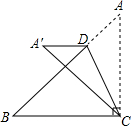 如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.
如图,在Rt△ABC中BC=AC=4,D是斜边AB上的一个动点,把△ACD沿直线CD折叠,点A落在同一平面内的A′处,当A′D垂直于Rt△ABC的直角边时,AD的长为4$\sqrt{2}$-4或4.