题目内容
2．某抛物线有以下性质：①开口向下；②对称轴是y轴；③与x轴不相交；④最高点是原点．其中y=-2x2具有的性质是①②④．（填序号）分析 此题应从二次函数的基本形式入手，它符合y=ax2的基本形式，根据它的性质，进行解答．
解答 解：∵a=-2＜0，
∴开口向下，有最高点，顶点坐标（0，0），对称轴是y轴，
∴y=-2x2具有的性质是①②④，
故答案为：①②④．
点评 此题主要考查了二次函数的图象性质，熟练掌握y=ax2的性质是解答此题的关键．
练习册系列答案
相关题目
12．已知直线y=ax+b（a≠0）经过点A（-3，0）和点B（0，2），那么关于x的方程ax+b=0的解是（ ）
| A． | x=-3 | B． | x=-1 | C． | x=0 | D． | x=2 |
17．下列事件中，为必然事件的是（ ）
| A． | 购买一张彩票，中奖 | |
| B． | 在标准状况下，加热到100℃时，水沸腾 | |
| C． | 任意画一个三角形，其内角和是360° | |
| D． | 射击运动员射击一次，命中靶心 |
7．
如图，在数轴上，点A表示$\sqrt{2}$，点B表示5.1，则A，B之间表示整数的点共有（ ）
如图，在数轴上，点A表示$\sqrt{2}$，点B表示5.1，则A，B之间表示整数的点共有（ ）| A． | 6个 | B． | 5个 | C． | 4个 | D． | 3个 |
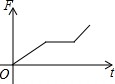
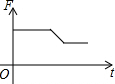
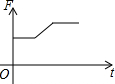
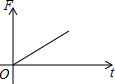
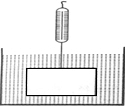如图，挂在弹簧秤上的长方体铁块浸没在水中，提着弹簧匀速上移，直至铁块浮出水面停留在空中（不计空气阻力），弹簧秤的读数F（kg）与时间t（s）的函数图象大致是（ ）
