题目内容
4．
如图，已知AB，CD相交于点O，OE⊥CD于O，∠AOC=35°，则∠BOE的度数是（ ）| A． | 35° | B． | 55° | C． | 125° | D． | 145° |
分析 先根据垂足求得∠DOE的度数，再根据对顶角相等，求得∠BOD的度数，最后计算∠BOE的度数．
解答 解：∵OE⊥CD，
∴∠DOE=90°，
∵∠AOC=35°，
∴∠BOD=35°，
∴∠BOE=∠BOD+∠DOE=35°+90°=125°．
故选（C）
点评 本题主要考查了垂线以及对顶角，解题的关键是正确利用角的和差关系，解法不唯一，也可以利用邻补角进行计算求解．邻补角、对顶角都是相对于两个角而言，是指两个角的一种位置关系．
练习册系列答案
相关题目
15．在Rt△ABC中，∠C=90°，a=12，b=5，则c的长为（ ）
| A． | 13 | B． | 14 | C． | 15 | D． | 16 |
12．已知直线a∥b，点M到直线a的距离是5cm，到直线b的距离是3cm，那么直线a和b之间的距离是（ ）
| A． | 2cm | B． | 6cm | C． | 8cm | D． | 2cm或8cm |
19．64-（3a-2b）2分解因式的结果是（ ）
| A． | （8+3a-2b）（8-3a-2b） | B． | （8+3a+2b）（8-3a-2b） | C． | （8+3a+2b）（8-3a+2b） | D． | （8+3a-2b）（8-3a+2b） |
9．
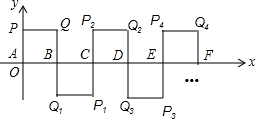如图所示，在平面直角坐标系中A（0，0），B（1，0），P（0，1），四边形ABQP是正方形，把正方形ABQP绕点B顺时针旋转180°，得到正方形CBQ1P1；把正方形CBQ1P1绕点C顺时针旋转180°，得到正方形CDQ2P2；依此类推，则旋转第2016次后，得到的正方形的顶点P2016的坐标为（ ）
如图所示，在平面直角坐标系中A（0，0），B（1，0），P（0，1），四边形ABQP是正方形，把正方形ABQP绕点B顺时针旋转180°，得到正方形CBQ1P1；把正方形CBQ1P1绕点C顺时针旋转180°，得到正方形CDQ2P2；依此类推，则旋转第2016次后，得到的正方形的顶点P2016的坐标为（ ）| A． | （2016，1） | B． | （2015，1） | C． | （2016，-1） | D． | （4032，1） |
13．如图所示，下列几何体中，主视图、左视图、俯视图都相同的是（ ）
| A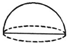． |  半球 | B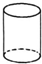． |  圆柱 | C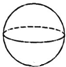． |  球 | D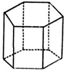． |  六棱柱 |