题目内容
1.(1)x2-8x=0;(2)2x2-3x-5=0.
分析 (1)利用因式分解法把方程化为x=0或x-8=0,然后解两个一次方程即可;
(2)利用十字相乘法把要求的式子进行因式分解,然后求解即可.
解答 解:(1)x2-8x=0,
x(x-8)=0,
x=0或x-8=0,
x1=0,x2=8;
(2)2x2-3x-5=0,
(2x-5)(x+1)=0,
x1=$\frac{5}{2}$,x2=-1.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
11.-2的绝对值是( )
| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -2 |
10.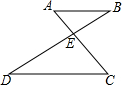 如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )
如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )
 如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )
如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{8}{125}$ |
11.下列判断中错误的是( )
| A. | 1-a-ab是二次三项式 | B. | -a2b2c的次数是5 | ||
| C. | $\frac{{a}^{2}+{b}^{2}}{ab}$是单项式 | D. | $\frac{3}{4}$πa2的系数是$\frac{3}{4}$π |