Question

3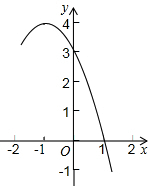．已知抛物线y=-x²+bx+c的部分图象如图所示．
（1）求b，c的值；
（2）当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减小？
（3）当y＜0时，直接写出x的取值范围．

Answer 1

分析 （1）由函数的图象可知c=3，把（1，0）代入抛物线的解析式即可求出b的值；
（2）由（1）中的抛物线解析式即可求出抛物线的对称轴，然后根据二次函数的性质即可求得xd的取值；
（3）根据抛物线与x轴的交点坐标及对称轴求出它与x轴的另一交点坐标，求当y＜0，x的取值范围就是求函数图象位于x轴的下方的图象相对应的自变量x的取值范围．

解答 解：（1）由函数的图象可知c=3，把（1，0）代入y=-x²+bx-c得，b=-2，
所以b=-2，c=-3；
（2）由（1）可知y=-x²-2x+3，
∴y=-（x+1）²+4，
∴对称轴为直线x=-1，
∵a=-1，
∴当x＜-1时，y随x的增大而增大，当x＞-1时，y随x的增大而减小；
（3）由图象知，抛物线与x轴交于（1，0），对称轴为x=-1，
∴抛物线与x轴的另一交点坐标为（-3，0），
∵y＜0时，函数的图象位于x轴的下方，
∴x＞1或x＜-3．

点评 本题考查了待定系数法求二次函数的解析式以及二次函数的性质，求得对称轴和二次函数与x轴的交点坐标是解题的关键．