题目内容
12.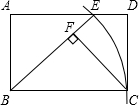 如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交AD边于点E,连接BE,过C点作CF⊥BE,垂足为F
如图,在矩形ABCD中,以点B为圆心,BC长为半径画弧,交AD边于点E,连接BE,过C点作CF⊥BE,垂足为F(1)猜想线段BF与图中现有的哪一条线段相等,并加以证明.
(2)求证:FE=ED.
分析 (1)结论:BF=AE.只要证明△AEB≌△FBC,即可解决问题.
(2)连接EC,只要证明Rt△CEF≌Rt△CED,即可.
解答 (1)解:结论:BF=AE.
理由:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠BFC=90°,AE∥CB,
∴∠AEB=∠CBF,
在△AEB和△FBC中,
$\left\{\begin{array}{l}{∠A=∠BFC}\\{∠AEB=∠CBF}\\{BE=BC}\end{array}\right.$,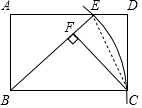
∴△AEB≌△FBC,
∴AE=BF.
(2)证明:连接EC.
∵四边形ABCD是矩形,
∴AB=CD,∠D=∠CFE=90°
∵△AEB≌△FBC,
∴AB=CF,
∵AB=CD,
在Rt△CEF和Rt△CED中,
$\left\{\begin{array}{l}{CE=CE}\\{CF=CD}\end{array}\right.$,
∴Rt△CEF≌Rt△CED,
∴EF=ED.
点评 本题考查矩形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.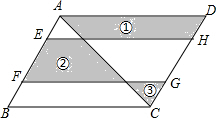 如图,E,F是?ABCD的边AB上的两动点,且EF=AE+BF,过E,F作EH∥FG∥AD交CD于点H,G,连接AC得图中所示的①,②,③三块阴影,若其中①,③的面积分别为5,2,则②的面积为7.
如图,E,F是?ABCD的边AB上的两动点,且EF=AE+BF,过E,F作EH∥FG∥AD交CD于点H,G,连接AC得图中所示的①,②,③三块阴影,若其中①,③的面积分别为5,2,则②的面积为7.
 如图,E,F是?ABCD的边AB上的两动点,且EF=AE+BF,过E,F作EH∥FG∥AD交CD于点H,G,连接AC得图中所示的①,②,③三块阴影,若其中①,③的面积分别为5,2,则②的面积为7.
如图,E,F是?ABCD的边AB上的两动点,且EF=AE+BF,过E,F作EH∥FG∥AD交CD于点H,G,连接AC得图中所示的①,②,③三块阴影,若其中①,③的面积分别为5,2,则②的面积为7.
17.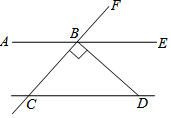 如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )
如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )
 如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )
如图,AB∥CD,DB⊥BC,∠BDC=50°,则∠FBE的度数是( )| A. | 50° | B. | 45° | C. | 40° | D. | 30° |
4.过八边形的一个顶点最多可以引_______条对角线( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
2.∠1与∠2是两条直线被第三条直线所截的同位角,若∠1=50°,则∠2为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 不能确定 |
 如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2)
如图,直角三角形ABC以1cm/s的速度沿直线l向正方形DEFG移动,直到AB与DC重合时停止,移动前如图①所示,∠B=90°,AB=8cm,BC=6cm,正方形的边长为8cm.设移动x(s)时,三角形与正方形重叠部分的面积y(m2) 如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?