题目内容
9.将抛物线y=$\frac{1}{2}$x2-6x+21绕原点旋转180°后,所得新抛物线的解析式为( )| A. | y=$\frac{1}{2}$x2+6x+21 | B. | y=-$\frac{1}{2}$x2+6x-21 | C. | y=-$\frac{1}{2}$x2-6x+21 | D. | y=-$\frac{1}{2}$x2-6x-21 |
分析 先将原抛物线解析式化为顶点式,将其绕顶点旋转180°后,开口大小和顶点坐标都没有变化,变化的只是开口方向,再根据关于原点对称的两点的横坐标纵坐标都互为相反数得出所求新抛物线的解析式.
解答 解:y=$\frac{1}{2}$x2-6x+21,
=$\frac{1}{2}$(x2-12x+36)-18+21,
=$\frac{1}{2}$(x-6)2+3,
将原抛物线绕原点旋转180°后,得y=-$\frac{1}{2}$(x+6)2-3,
即:y=-$\frac{1}{2}$x2-6x-21,
故选:D.
点评 此题主要考查了根据二次函数的图象的变换求抛物线的解析式.关键是掌握关于原点对称的两点的横坐标纵坐标都互为相反数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知某三角形的周长为3m-n,其中两边的和为m+n-4,则此三角形第三边的长为( )
| A. | 2m-4 | B. | 2m-2n-4 | C. | 2m-2n+4 | D. | 4m-2n+4 |
4.下列是二次函数的是( )
| A. | y=ax2+bx+c | B. | y=$\frac{1}{{x}^{2}}$+x | C. | y=x2-(x+7)2 | D. | y=(x+1)(2x-1) |
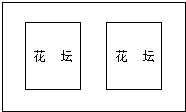 某中学为了美化校园,决定在一个长是宽1.5倍的矩形空地中间修建两个全等的矩形花坛(如图所示),在空白的地带修建宽都为2米的花径,花径的面积占整个空地面积的$\frac{9}{25}$,求这块空地的长为多少米?
某中学为了美化校园,决定在一个长是宽1.5倍的矩形空地中间修建两个全等的矩形花坛(如图所示),在空白的地带修建宽都为2米的花径,花径的面积占整个空地面积的$\frac{9}{25}$,求这块空地的长为多少米?