Question

19．在△ABC中，AC=BC，∠ACB=90°，CE是过C点的一条直线，AD⊥CE于D，BE⊥CE于E，DE=4cm，AD=2cm，则BE=6或2cm．

Answer 1

分析 ①画出图形，由题中AC=BC可得△ACD≌△CBE，得出对应线段CE=AD，CD=BE，进而可得出结论；②通过全等推出CE=AD，CD=BE，进而得出答案．
．证明方法同上

解答 解：分为两种情况：
①如图1，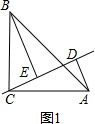
∵AD⊥CE，∠BCA=90°，
∴∠ADC=∠BCA=90°，
∴∠DCA+∠BCE=90°，∠DCA+∠DAC=90°，
∴∠DAC=∠BCE，
∵AD⊥CE，BE⊥CE，
∴∠ADC=∠BEC=90°，
在△ACD和△CBE中，
∵$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠DAC=∠BCE}\\{AC=BC}\end{array}\right.$，
∴△ACD≌△CBE（AAS）
∴CE=AD=2cm，CD=BE，
BE=CD=CE+DE=2cm+4cm=6cm；

②如图2，
∵在△EBC和△DAC中
$\left\{\begin{array}{l}{∠BEC=∠ADC}\\{∠DAC=∠BCE}\\{AC=BC}\end{array}\right.$
∴△ACD≌△CBE（AAS），
∴CE=AD=2cm，BE=CD，
∴BE=CD=DE-AD=4cm-2cm=2cm，
故答案为：6或2．

点评 本题主要考查了全等三角形的判定及性质问题，能求出符合的所有情况是解此题的关键，题目比较好．