题目内容
 如图,在⊙O中,AB,AC是互相垂直且相等的两条弦,若AB=2cm,则⊙O的半径OA为
如图,在⊙O中,AB,AC是互相垂直且相等的两条弦,若AB=2cm,则⊙O的半径OA为考点:垂径定理,勾股定理
专题:
分析:如图,作辅助线,证明BC为⊙O的直径;求出BC的长度,即可解决问题.
解答: 解:如图,连接BC;
解:如图,连接BC;
∵AB⊥AC,
∴∠BAC=90°,
∴BC为⊙O的直径;
由勾股定理得:
BC2=AC2+BC2,而AB=AC=2,
∴BC=2
(cm).
∴OA=
cm.
故答案为
cm.
 解:如图,连接BC;
解:如图,连接BC;∵AB⊥AC,
∴∠BAC=90°,
∴BC为⊙O的直径;
由勾股定理得:
BC2=AC2+BC2,而AB=AC=2,
∴BC=2
| 2 |
∴OA=
| 2 |
故答案为
| 2 |
点评:该题主要考查了圆周角定理、勾股定理及其应用问题;灵活运用圆周角定理、勾股定理来解题是关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
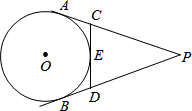 如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )
如图所示,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=15,则△PCD的周长为( )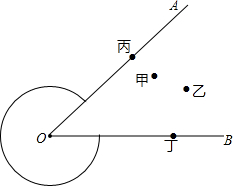 甲乙丙丁四位同学在铅球场地做接力游戏,其中丙在OA边,丁在OB边.游戏规则是,甲将接力棒传给丙,丙传给丁,丁传给乙,乙最后丁跑回甲处.那么丙丁两人站在何处,才能使四人的路程和最短?(请画出路线,并保留作图痕迹,作法不用写)
甲乙丙丁四位同学在铅球场地做接力游戏,其中丙在OA边,丁在OB边.游戏规则是,甲将接力棒传给丙,丙传给丁,丁传给乙,乙最后丁跑回甲处.那么丙丁两人站在何处,才能使四人的路程和最短?(请画出路线,并保留作图痕迹,作法不用写) 如图,在平面直角坐标系xOy中,已知A(2,4),B(6,6),C(8,2),求四边形OABC的面积.
如图,在平面直角坐标系xOy中,已知A(2,4),B(6,6),C(8,2),求四边形OABC的面积. 如图,在△ABC中,DE∥BC.
如图,在△ABC中,DE∥BC. 如图,AD⊥BD,AE平分∠BAC,∠B=30°,∠ACD=70°,则∠CAE的度数是
如图,AD⊥BD,AE平分∠BAC,∠B=30°,∠ACD=70°,则∠CAE的度数是