题目内容
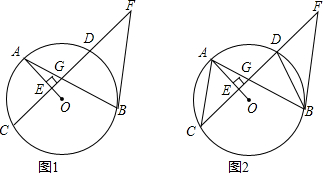
已知在两个同心圆中,大圆的弦AB,AC分别与小圆相切于点D,E.求证:DE∥BC且DE=
BC.
| 1 |
| 2 |
考点:切线的性质,三角形中位线定理,垂径定理
专题:证明题
分析:连接OD,OE,根据切线性质求出OD⊥AB,OE⊥AC,根据垂径定理求出AD=BD,AE=CE,根据三角形的中位线定理求出即可.
解答: 证明:连接OD、OE,
证明:连接OD、OE,
则OD⊥AB,OE⊥AC,
由垂径定理得:AD=BD,AE=CE,
∴DE∥BC且DE=
BC.
 证明:连接OD、OE,
证明:连接OD、OE,则OD⊥AB,OE⊥AC,
由垂径定理得:AD=BD,AE=CE,
∴DE∥BC且DE=
| 1 |
| 2 |
点评:本题考查了三角形的中位线定理,垂径定理,切线的性质等知识点的应用,主要培养学生运用定理进行推理的能力,题型较好.

练习册系列答案
相关题目
已知关于x的方程4x-5m=9的解x=m,则m的值是( )
| A、-9 | B、9 | C、1 | D、-1 |
某服装店把原价为100元的衣服提价10%后,再降价10%销售,则该衣服的价格为( )
| A、100元 | B、1元 |
| C、50元 | D、99元 |
 如图,在⊙O中,AB,AC是互相垂直且相等的两条弦,若AB=2cm,则⊙O的半径OA为
如图,在⊙O中,AB,AC是互相垂直且相等的两条弦,若AB=2cm,则⊙O的半径OA为