题目内容
1.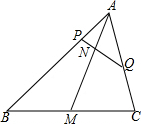 如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.(1)求证:$\frac{PB}{PA}$+$\frac{QC}{QA}$=$\frac{2MN}{NA}$;
(2)若$\frac{AP}{PB}$=m,$\frac{AQ}{QC}$=n,求$\frac{MN}{NA}$的值.
分析 (1)分别过点B,C作PQ的平行线,交AM的延长线于D,E则△BDM≌△CEM,利用PQ∥BD,得到比例式,即可证得结论;
(2)利用(1)的结论即可求得$\frac{MN}{NA}$的值.
解答  (1)证明:分别过点B,C作PQ的平行线,交AM于D,E,
(1)证明:分别过点B,C作PQ的平行线,交AM于D,E,
∴∠BDE=∠CED,
在△BDM与△CEM中,$\left\{\begin{array}{l}{∠BDE=∠CEM}\\{∠BMD=∠EMC}\\{BM=CM}\end{array}\right.$,
∴△BMD≌△CME,
∴DM=EM,
∵PQ∥BD,
∴$\frac{PB}{PA}=\frac{ND}{AN}$,
同理:$\frac{QC}{QA}=\frac{NE}{AN}$,
∴$\frac{PB}{PA}$+$\frac{QC}{QA}$=$\frac{2MN}{NA}$;
(2)解:由(1)证得$\frac{PB}{PA}$+$\frac{QC}{QA}$=$\frac{2MN}{NA}$;
∵$\frac{AP}{PB}$=m,$\frac{AQ}{QC}$=n,
∴$\frac{1}{m}+\frac{1}{n}$=$\frac{2MN}{AN}$=$\frac{m+n}{mn}$,
∴$\frac{MN}{NA}$=$\frac{m+n}{2mn}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.阅读材料:在△ABC中,有一点P,当P1、A、B、C没有任何三点在同一直线上,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互补重叠的小三角形的个数情况怎样?请观察图形和表格填空.表格中的空白处应填( )

| △ABC内点的个数 | 1 | 2 | 3 | … | 12 |
| 构成不重叠的小三角形的个数 | 3 | 5 | 7 | … |

| A. | 21 | B. | 23 | C. | 25 | D. | 28 |
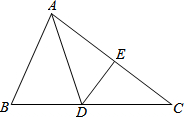 如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长.
如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长.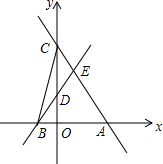 直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
 以△ABC的边BC为一边向三角形外侧作正方形BDEC,连结AD、AE分别交BC于点F、G,过点F、G分别作BC的垂线交AB、AC于点H、K,试判断四边形HFGK的形状.
以△ABC的边BC为一边向三角形外侧作正方形BDEC,连结AD、AE分别交BC于点F、G,过点F、G分别作BC的垂线交AB、AC于点H、K,试判断四边形HFGK的形状. 如图,在Rt△ABC中,∠A=30°,点D是斜边AB的中点,点G是Rt△ABC的重心,GE⊥AC于点E.若BC=6cm,则GE=2cm.
如图,在Rt△ABC中,∠A=30°,点D是斜边AB的中点,点G是Rt△ABC的重心,GE⊥AC于点E.若BC=6cm,则GE=2cm.