题目内容
20.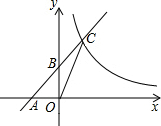 如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点C,O为坐标原点,连接OC.若△AOC的面积为1,则k的值为2.
如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点C,O为坐标原点,连接OC.若△AOC的面积为1,则k的值为2.
分析 根据直线的解析式求得A点的坐标,根据三角形的面积求得C的纵坐标,代入直线解析式即可求得坐标,然后根据待定系数法求得即可.
解答 解:由一次函数y=x+1可知,A(-1,0),B(0,1),
∴OA=1,
∵S△AOC=1,
∴$\frac{1}{2}$OA•|yC|=1,
∴yC=2,
代入y=x+1得2=x+1,解得x=1,
∴C(1,2),
∵C点在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴2=$\frac{k}{1}$,解得k=2.
故答案为2.
点评 本题考查了反比例函数和一次函数的交点问题以及待定系数法求反比例函数的解析式,求得C的坐标是本题的关键.

练习册系列答案
相关题目
10.已知关于x的不等式组$\left\{\begin{array}{l}{x-m≥n}\\{2x-m<2n+1}\end{array}\right.$的解集为3≤x<5,则m-n的值是( )
| A. | -9 | B. | 9 | C. | 5 | D. | -5 |
11. 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )| A. | 每月阅读数量的平均数是50 | B. | 众数是42 | ||
| C. | 中位数是58 | D. | 每月阅读数量超过40的有4个月 |
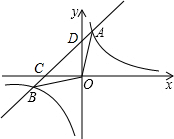 已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.
已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.
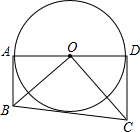 如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=$\frac{16}{3}$
如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=$\frac{16}{3}$ 如图是某教室里日光灯的四个控制开关(分别记为A、B、C、D),每个开关分别控制一排日光灯(开关序号与日光灯的排数序号不一定一致).某天上课时,王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关.
如图是某教室里日光灯的四个控制开关(分别记为A、B、C、D),每个开关分别控制一排日光灯(开关序号与日光灯的排数序号不一定一致).某天上课时,王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关.