题目内容
9.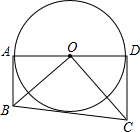 如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=$\frac{16}{3}$
如图,⊙O的直径AD=8,AB、CD是⊙O的两条切线,AB=3,CD=$\frac{16}{3}$(1)求证:△ABO∽△DOC;
(2)求证:BC是⊙O的切线.
分析 (1)根据AD,BC为圆的切线,利用切线的性质得到∠OAD=∠OBC=90°,进而求得$\frac{AB}{OA}$=$\frac{OD}{CD}$=$\frac{3}{4}$,然后根据两边对应成比例且夹角相等的三角形相似即可得证;
(2)过O作OE⊥BC,交BC于点E,根据(1)中两相似三角形,利用相似三角形的对应角相等得到∠ABO=∠COD,进而求得∠BOC=90°,然后根据∠OBE=∠CBO,∠OEB=∠BOC=90°,得到△BOE∽△BCO,由相似三角形的对应边成比例得到OE=4=OA,即可确定出BC为圆O的切线.
解答 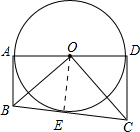 (1)证明:∵AD、BC是⊙O的两条切线,
(1)证明:∵AD、BC是⊙O的两条切线,
∴∠OAD=∠OBC=90°,
∵AB=3,CD=$\frac{16}{3}$,AD=8,
∴OA=OD=4,
∴$\frac{AB}{OA}$=$\frac{3}{4}$,$\frac{OD}{CD}$=$\frac{4}{\frac{16}{3}}$=$\frac{3}{4}$,
∴$\frac{AB}{OA}$=$\frac{OD}{CD}$,
∴△ABO∽△DOC;
(3)证明:过O作OE⊥BC,交BC于点E,
∵△ABO∽△DOC,
∴∠ABO=∠COD,
∵∠ABO+∠AOB=90°,
∴∠AOB+∠COD=90°,
∵∠BOC=90°,
∵∠OBE=∠CBO,∠OEB=∠BOC=90°,
∴△BOE∽△BCO,
∴$\frac{OE}{OC}$=$\frac{OB}{BC}$,
由∵OB=$\sqrt{{3}^{2}+{4}^{2}}$=5,OC=$\sqrt{{4}^{2}+(\frac{16}{3})^{2}}$=$\frac{20}{3}$,
∴BC=$\sqrt{{5}^{2}+(\frac{20}{3})^{2}}$=$\frac{25}{3}$,
∴$\frac{OE}{\frac{20}{3}}$=$\frac{5}{\frac{25}{3}}$,
∴OE=4=OA,
∴BC是⊙O切线.
点评 此题考查了切线的判定与性质,涉及的知识有:相似三角形的判定与性质,勾股定理,熟练掌握切线的判定与性质是解本题的关键.

 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案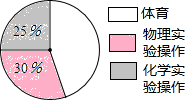 赤峰市对九年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三个科目共1000名学生的成绩进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如表及图所示.
赤峰市对九年级学生的体育、物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A,B,C,D四个等级.现抽取这三个科目共1000名学生的成绩进行统计分析,其中A,B,C,D分别表示优秀,良好,合格,不合格四个等级.相关数据统计如表及图所示.| 等级 人数 科目 | A | B | C | D |
| 物理实验操作 | 120 | 7 | 90 | 20 |
| 化学实验操作 | 90 | 110 | 30 | 20 |
| 体育 | 123 | 140 | 160 | 27 |
(2)赤峰市共有40000名学生参加测试,试估计该市九年级学生化学实验操作合格及合格以上大约有多少人?
(3)在这40000名学生中,体育成绩不合格的大约有多少人?
| A. | 25 | B. | -25 | C. | $\frac{1}{25}$ | D. | -$\frac{1}{25}$ |
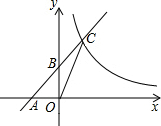 如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点C,O为坐标原点,连接OC.若△AOC的面积为1,则k的值为2.
如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点C,O为坐标原点,连接OC.若△AOC的面积为1,则k的值为2.