题目内容
15. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=$\sqrt{3}$,则BC=3$\sqrt{3}$.
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=$\sqrt{3}$,则BC=3$\sqrt{3}$.
分析 根据角平分线的性质即可求得CD的长,然后在直角△BDE中,根据30°的锐角所对的直角边等于斜边的一半,即可求得BD长,则BC即可求得.
解答 解:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=$\sqrt{3}$,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2$\sqrt{3}$,
∴BC=CD+BD=$\sqrt{3}$+2$\sqrt{3}$=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题考查了角的平分线的性质以及直角三角形的性质,30°的锐角所对的直角边等于斜边的一半,理解性质定理是关键.

练习册系列答案
相关题目
4. 如图,OC是∠AOB的平分线,OD是∠BOC的平分线,若∠AOB=120°,则∠AOD的度数为( )
如图,OC是∠AOB的平分线,OD是∠BOC的平分线,若∠AOB=120°,则∠AOD的度数为( )
 如图,OC是∠AOB的平分线,OD是∠BOC的平分线,若∠AOB=120°,则∠AOD的度数为( )
如图,OC是∠AOB的平分线,OD是∠BOC的平分线,若∠AOB=120°,则∠AOD的度数为( )| A. | 30° | B. | 50° | C. | 60° | D. | 90° |
 如图所示,直角三角形AOB的周长为100,在其内部有6个小直角三角形,则这6个小直角三角形的周长之和为100.
如图所示,直角三角形AOB的周长为100,在其内部有6个小直角三角形,则这6个小直角三角形的周长之和为100.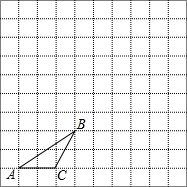 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点). 已知点A在数轴上的位置如图,如果点B也在同一条数轴上,且到点A的距离为3,则点B所表示的数是-5或1.
已知点A在数轴上的位置如图,如果点B也在同一条数轴上,且到点A的距离为3,则点B所表示的数是-5或1.