题目内容
16.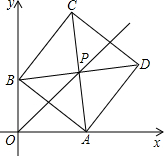 在平面直角坐标系xOy中,正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在直线y=x上.
在平面直角坐标系xOy中,正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在直线y=x上.
分析 作PE⊥x轴于E,PF⊥y轴于F,只要证明PE=PF即可解决问题.
解答 解: 作PE⊥x轴于E,PF⊥y轴于F,则四边形PEOF是矩形,
作PE⊥x轴于E,PF⊥y轴于F,则四边形PEOF是矩形,
∵四边形ABCD是正方形,
∴∠EPF=∠APB=90°,PB=PA,
∴∠EPA=∠FPB,∵∠PEA=∩PFB,
∴△PEA≌△PFB,
∴PE=PF,
∴∠POE=∠POF,
∴无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在直线y=x上.
点评 本题考查的是一次函数综合题,涉及到全等三角形的判定与性质、等腰直角三角形的性质及正方形的判定与性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
7.计算(-2)2012+(-2)2013的结果是( )
| A. | 22013 | B. | -22012 | C. | -22013 | D. | -2 |
6.已知点A(-3,y1),B(-1,y2),C(2,y3)在函数y=-x2的图象上,则y1、y2、y3的大小关系为( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
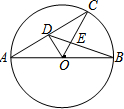 如图,AB是⊙O的直径,AC是弦.OD⊥AC于D,OC与BD交于E,若BD=6,则DE等于( )
如图,AB是⊙O的直径,AC是弦.OD⊥AC于D,OC与BD交于E,若BD=6,则DE等于( )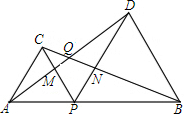 如图,点P为线段AB上的一点,分别以点AP,BP构造等边三角形,连接AD和BC交于点Q,AD与PC交于点M,BC与PD交与点N.
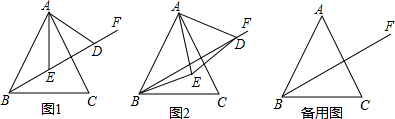
如图,点P为线段AB上的一点,分别以点AP,BP构造等边三角形,连接AD和BC交于点Q,AD与PC交于点M,BC与PD交与点N.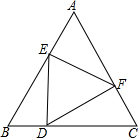 如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发.设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程中始终保持∠EDF=60°.
如图,△ABC是边长为9cm的等边三角形,D、E是边BC、BA上的动点,D点由B点开始以1cm/秒的速度向C点运动,E点由B点开始以2cm/秒的速度向A点运动,D、E同时出发.设运动时间为t,当其中一点到达边的端点时,运动便停止,在运动过程中始终保持∠EDF=60°. 如图,在平面直角坐标系xOy中,A点在x轴的负半轴上,其坐标为(-6.0),C点在y轴的正半轴上,其坐标为(0,8),以OA,OC为邻边在第二象限内作长方形OABC
如图,在平面直角坐标系xOy中,A点在x轴的负半轴上,其坐标为(-6.0),C点在y轴的正半轴上,其坐标为(0,8),以OA,OC为邻边在第二象限内作长方形OABC