题目内容
1.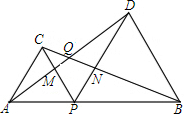 如图,点P为线段AB上的一点,分别以点AP,BP构造等边三角形,连接AD和BC交于点Q,AD与PC交于点M,BC与PD交与点N.
如图,点P为线段AB上的一点,分别以点AP,BP构造等边三角形,连接AD和BC交于点Q,AD与PC交于点M,BC与PD交与点N.(1)求证:AD=BC,并求出AD与BC的夹角∠DQB的大小.
(2)猜想PM与PN的数量关系,并证明.
分析 (1)首先根据ASA证明△APD≌△CPB,证明∠PBC=∠PDA,利用三角形的外角的性质即可证得;
(2)首先证明△PBN≌△PDM,证明PM=PN.
解答 解:(1)∵△APC与△PBD为等边三角形,
∴∠APC=∠BPD=60°,AP=PC,PB=PD,
∴∠APD=∠CPB,
在△APD和CPB中,$\left\{\begin{array}{l}{AP=CP}\\{∠APD=∠CPB}\\{PD=PB}\end{array}\right.$,
∴△APD≌△CPB,
∴∠PBC=∠PDA,
∴∠DQB=∠DAB+∠ABQ=∠DAB+∠ADP=∠DPB=60°;
(2)∵△APD≌△CPB.
∴∠PBN=∠PDM,
又∵△APC和△PBD都是等边三角形,且点A、P、B在同一条直线上,
∴∠CPD=180°-∠APC-∠BPD=60°=∠BPD,
在△PBN和△PDM中,$\left\{\begin{array}{l}{∠PBC=∠PDM}\\{PB=PD}\\{∠CPD=∠BPD}\end{array}\right.$,
∴△PBN≌△PDM(ASA),
∴PM=PN.
点评 本题考查的是等边三角形的判定与性质及全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.

练习册系列答案
相关题目
11. 如图是一个指示标志,它的左视图是( )
如图是一个指示标志,它的左视图是( )
 如图是一个指示标志,它的左视图是( )
如图是一个指示标志,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
10.下列各式中不是整式的是( )
| A. | 3x | B. | $\frac{1}{x}$ | C. | $\frac{xy}{2}$ | D. | x-3y |
11.关于x的一元二次方程:x2+2x+2a-1=0的一个解是x=1,则a=( )
| A. | -1 | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
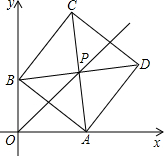 在平面直角坐标系xOy中,正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在直线y=x上.
在平面直角坐标系xOy中,正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限.求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在直线y=x上.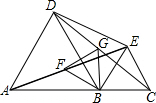 A,B,C在一条直线上,△ABD与△BCE为等边三角形,连AE,CD,F为AE的中点,G为CD的中点,判断△BFG的形状.
A,B,C在一条直线上,△ABD与△BCE为等边三角形,连AE,CD,F为AE的中点,G为CD的中点,判断△BFG的形状.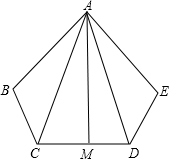 如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M,求证:CM=MD.
如图,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为M,求证:CM=MD.