题目内容
1．已知线段AB=4cm，过点B作BC⊥AB，且BC=2cm，连结AC，以C为圆心，CB为半径作弧，交AC于D；以A为圆心，AD为半径作弧，交AB于P，量一量线段AP的长，约为（ ）| A． | 2 cm | B． | 2.5 cm | C． | 3 cm | D． | 3.5 cm |
分析 根据题意，作出图形．根据勾股定理求得AC的长度，则AP=AD=AC-CD．
解答 
解：如图，AB=4cm，BC=2cm，BC⊥AB，
在Rt△ABC中，由勾股定理，得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$cm．
又∵CD=BC=2cm，
∴AP=AD=AC-CD=2$\sqrt{5}$-2≈2.5cm．
故选：B．
点评 本题考查了勾股定理．根据勾股定理求得斜边AC的长度是解题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
18．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，种植花卉的利润y2与投资量x的平方成正比例关系，并得到了表格中的数据．
（1）分别求出利润y1与y2关于投资量x的函数关系式；
（2）如果这位专业户以8万元资金投入种植花卉和树木，设他投入种植花卉金额m万元，种植花卉和树木共获利利润W万元，直接写出W关于m的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
（3）若该专业户想获利不低于22万，在（2）的条件下，直接写出投资种植花卉的金额m的范围．
| 投资量x（万元） | 2 |
| 种植树木利润y1（万元） | 4 |
| 种植花卉利润y2（万元） | 2 |
（2）如果这位专业户以8万元资金投入种植花卉和树木，设他投入种植花卉金额m万元，种植花卉和树木共获利利润W万元，直接写出W关于m的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
（3）若该专业户想获利不低于22万，在（2）的条件下，直接写出投资种植花卉的金额m的范围．
12．按照下面的操作步骤，若输入x=-4，则输出的值为（ ）
| A． | 3 | B． | -3 | C． | -5 | D． | 5 |
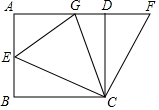如图1，在边长4的正方形ABCD中，E是AB边上一动点（不与A、B重合），F是AD延长线上一点，且满足DF=BE，以CE为边作∠ECG=45°，交AD于点G．
16．已知一个三角形的三边长分别为$\sqrt{2}$，$\sqrt{6}$，2，则这个三角形的面积为（ ）
| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
如图，△ABC中，∠C=90°，∠BAC=30°，AB=8，AD平分∠BAC，点P，Q分别是AB，AD上的动点，则PQ+BQ的最小值是4．