题目内容
14.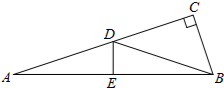 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.(1)若AD=15,cos∠BDC=$\frac{4}{5}$,求AC的长和tanA的值;
(2)若∠BDC=30°,求tan15°的值.(结果保留根号)
分析 (1)由线段垂直平分线的性质得DB=DA=15,再根据余弦的定义得到cos∠BDC=$\frac{CD}{BD}$=$\frac{4}{5}$,则DC=12,根据勾股定理可计算出BC=9,然后在Rt△ACB中,根据正切的定义求解;
(2)设AD=t,则DB=t,在Rt△DCB中根据含30°角的直角三角形的性质得到BC=$\frac{1}{2}$t,DC=$\frac{\sqrt{3}}{2}$t,再证明∠A=15°,然后根据正切的定义即可求出tan15°=tanA=$\frac{BC}{AC}$=$\frac{\frac{1}{2}t}{(1+\frac{\sqrt{3}}{2})t}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$.
解答  解:(1)∵DE垂直平分AB,
解:(1)∵DE垂直平分AB,
∴DB=DA=15,
∵在Rt△DCB中,cos∠BDC=$\frac{CD}{BD}$=$\frac{4}{5}$,
∴$\frac{CD}{15}$=$\frac{4}{5}$,
∴DC=12,
∴BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=9.
在Rt△ACB中,AC=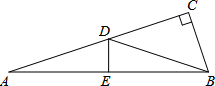 AD+CD=27,
AD+CD=27,
∴tanA=$\frac{BC}{AC}$=$\frac{9}{27}$=$\frac{1}{3}$;
(2)设AD=t,则DB=t,
∵在Rt△DCB中,∠C=90°,∠BDC=30°,
∴BC=$\frac{1}{2}$t,DC=$\frac{\sqrt{3}}{2}$t,
∵AD=BD,
∴∠A=∠ABD,
∵∠A+∠ABD=∠BDC=30°,
∴∠A=∠ABD=15°.
∵在Rt△ACB中,∠C=90°,AC=AD+DC=t+$\frac{\sqrt{3}}{2}$t=(1+$\frac{\sqrt{3}}{2}$)t,
∴tan15°=tanA=$\frac{BC}{AC}$=$\frac{\frac{1}{2}t}{(1+\frac{\sqrt{3}}{2})t}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$.
点评 本题考查了解直角三角形、勾股定理以及锐角三角函数的定义.求BC的长度时,利用“线段的垂直平分线上的点到线段的两个端点的距离相等”求得BD的长度是解答(1)的关键所在.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案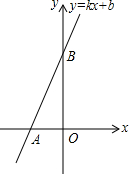 如图,直线y=kx+b交坐标轴于A(-2,0),B(0,4)两点,则不等式kx+b<0的解集为( )
如图,直线y=kx+b交坐标轴于A(-2,0),B(0,4)两点,则不等式kx+b<0的解集为( )| A. | x<-2 | B. | x>-2 | C. | x>2 | D. | x<2 |
 在下列四种图形变换中,如图图案包含的变换是( )
在下列四种图形变换中,如图图案包含的变换是( )| A. | 旋转和轴对称 | B. | 轴对称和平移 | ||
| C. | 平移和旋转 | D. | 平移、旋转和轴对称 |
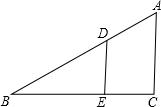 如图,D为直角三角形ABC斜边上一点,DE⊥BC于E点,BE=AC,若BD=$\frac{1}{2}$厘米,DE+BC=1厘米,试求∠B的大小.
如图,D为直角三角形ABC斜边上一点,DE⊥BC于E点,BE=AC,若BD=$\frac{1}{2}$厘米,DE+BC=1厘米,试求∠B的大小.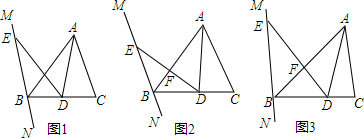
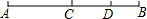 如图线段AB,C是线段AB的中点,点D在CB上,且AD=6.5cm,DB=1.5cm,则线段CD=2.5cm.
如图线段AB,C是线段AB的中点,点D在CB上,且AD=6.5cm,DB=1.5cm,则线段CD=2.5cm.
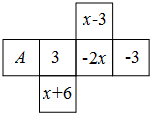 如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体相对的两个面所标注的值均互为相反数,求字母A所标注的值.
如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体相对的两个面所标注的值均互为相反数,求字母A所标注的值.