题目内容
5.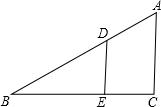 如图,D为直角三角形ABC斜边上一点,DE⊥BC于E点,BE=AC,若BD=$\frac{1}{2}$厘米,DE+BC=1厘米,试求∠B的大小.
如图,D为直角三角形ABC斜边上一点,DE⊥BC于E点,BE=AC,若BD=$\frac{1}{2}$厘米,DE+BC=1厘米,试求∠B的大小.
分析 设BE=x厘米,则AC=x厘米,得出DE=$\sqrt{B{D}^{2}-B{E}^{2}}$=$\sqrt{\frac{1}{4}-{x}^{2}}$,求出△BED∽△BCA,得出比例式,代入得出关于x的方程,求出x,即可得出DE=$\frac{1}{2}$BD,即可得出答案.
解答 解:设BE=x厘米,则AC=x厘米,
∵BD=$\frac{1}{2}$厘米,DE+BC=1厘米,
∴DE=$\sqrt{B{D}^{2}-B{E}^{2}}$=$\sqrt{\frac{1}{4}-{x}^{2}}$,BC=1-$\sqrt{\frac{1}{4}-{x}^{2}}$,
∵D为直角三角形ABC斜边上一点,DE⊥BC于E点,
∴∠C=∠BED,
∵∠B=∠B,
∴△BED∽△BCA,
∴$\frac{DE}{AC}$=$\frac{BE}{BC}$,
∴$\frac{\sqrt{\frac{1}{4}-{x}^{2}}}{x}$=$\frac{x}{1-\sqrt{\frac{1}{4}-{x}^{2}}}$,
解得:x=$\frac{\sqrt{3}}{4}$(负数舍去),
即DE=$\frac{1}{4}$=$\frac{1}{2}$BD,
∴∠B=30°.
点评 本题考查了解直角三角形,含30°角的直角三角形的性质,根据题意列方程是解题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
6.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.实验数据如下表:
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是$\frac{1}{3}$0.;
(2)当x=7时,请用列表法或树状图法计算“和为8”的概率;并判断x=7是否可能.
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8”出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8”出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是$\frac{1}{3}$0.;
(2)当x=7时,请用列表法或树状图法计算“和为8”的概率;并判断x=7是否可能.
3.下列各式变形正确的是( )
| A. | 如果2x=2y+1,那么x=y+1 | B. | 如果2=5+3x,那么3x=5-2 | ||
| C. | 如果x-3=y-3,那么x=y | D. | 如果-8x=4,那么x=-2 |
15.某公司年前缴税20万元,今年缴税24.2万元.若该公司这两年的年均增长率相同,设这个增长率为x,则列方程( )
| A. | 20(1+x)3=24.2 | B. | 20(1-x)2=24.2 | C. | 20+20(1+x)2=24.2 | D. | 20(1+x)2=24.2 |
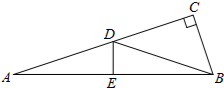 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与AC,AB的交点分别为D,E.