题目内容
 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,求证:∠ACB=
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,求证:∠ACB=| 1 |
| 2 |
考点:全等三角形的判定与性质
专题:证明题
分析:先根据SSS定理得出△ABC≌△DEB(SSS),故∠ACB=∠EBD,再根据∠AFB是△BFC的外角,可知∠AFB=∠ACB+∠EBD,由此可得出∠AFB=2∠ACB,故可得出结论.
解答:证明:在△ABC与△DEB中,
,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即∠ACB=
∠AFB.
|
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即∠ACB=
| 1 |
| 2 |
点评:本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
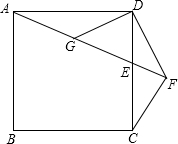 在正方形ABCD中,E为CD上一点,连接AE,过点C作CF⊥AF的延长线于点F,连接DF,过点D作DG⊥DF交AE于点G.
在正方形ABCD中,E为CD上一点,连接AE,过点C作CF⊥AF的延长线于点F,连接DF,过点D作DG⊥DF交AE于点G.(1)若DG=2,求FG的长;
(2)若E为CD的中点,求证:CF+EF=GE.
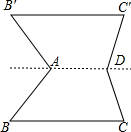 如图,在四边形ABCD中,AD∥BC.沿直线AD翻折四边形ABCD后可得四边形ADC′B′,那么四边形BCC′B′一定是( )
如图,在四边形ABCD中,AD∥BC.沿直线AD翻折四边形ABCD后可得四边形ADC′B′,那么四边形BCC′B′一定是( )| A、正方形 | B、菱形 | C、矩形 | D、梯形 |
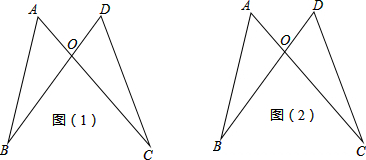
 已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D.
已知:如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CF.求证:∠B=∠D. 实数a,b,c在数轴上的位置如图,请化简:|c|-
实数a,b,c在数轴上的位置如图,请化简:|c|-