题目内容
11. 已知右表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n以及表中x的值.
已知右表内的各横行中,从第二个数起的数都比它左边相邻的数大m;各竖列中,从第二个数起的数都比它上边相邻的数大n.求m,n以及表中x的值.
分析 根据表内的各横行中,从第二个数起的数都比它左边相邻的数大m得出12+2m=18,解方程求出m的值;再由各竖列中,从第二个数起的数都比它上边相邻的数大n,得出(12+m)+3n=30,解方程求出n的值;进而求得x的值.
解答 解:∵各横行中,从第二个数起的数都比它左边相邻的数大m,
∴12+2m=18,
解得m=3.
又∵各竖列中,从第二个数起的数都比它上边相邻的数大n,
∴(12+m)+3n=30,
将m=3代入上述方程得 15+3n=30,
解得n=5.
此时x=12-2m+n=12-2×3+5=11.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.用四舍五入法对0.02015(精确到千分位)取近似数是( )
| A. | 0.02 | B. | 0.020 | C. | 0.0201 | D. | 0.0202 |
19.已知a-b=1,则代数式2a-2b-3的值是( )
| A. | 1 | B. | -1 | C. | 5 | D. | -5 |
16.如果y=$\sqrt{x-2}+\sqrt{2-x}$+3,那么yx的算术平方根是( )
| A. | 2 | B. | 3 | C. | 9 | D. | ±3 |
20.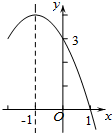 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
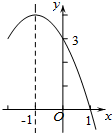 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为( )| A. | x=1 | B. | x=-1 | C. | x1=1,x2=-3 | D. | x1=1,x2=-4 |
1.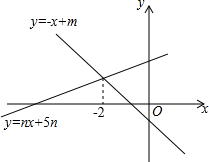 如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
 如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )
如图,直线y=-x+m与直线y=nx+5n(n≠0)的交点的横坐标为-2,则关于x的不等式-x+m>nx+5n>0的整数解为( )| A. | -5,-4,-3 | B. | -4,-3 | C. | -4,-3,-2 | D. | -3,-2 |
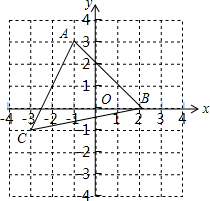 如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),B(2,0),C(-3,-1).
如图,在平面直角坐标系中有一个△ABC,顶点A(-1,3),B(2,0),C(-3,-1).