题目内容
某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,如果以单价28元销售,那么每月可售出44万件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高2元,销售量相应减少4万件.设销售量y(万件),销售单价为x(元)(利润=售价-制造成本).
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
考点:二次函数的应用
专题:
分析:(1)求出销售单价每提高1元,销售量减少2万件,然后表示出单件利润和销售量,再列式表示出利润即可;
(2)吧二次函数解析式整理成顶点式形式,再根据二次函数的最值问题解答;
(3)根据利润列出不等式求出单价的取值范围,再根据二次函数的增减性解答.
(2)吧二次函数解析式整理成顶点式形式,再根据二次函数的最值问题解答;
(3)根据利润列出不等式求出单价的取值范围,再根据二次函数的增减性解答.
解答:解:(1)∵销售单价每提高2元,销售量相应减少4万件,
∴销售单价每提高1元,销售量相应减少2万件,
∴z=(x-18)[44-2(x-28)]
=(x-18)(100-2x)
=-2x2+136x-1800;
(2)∵z=-2x2+136x-1800=-2(x-34)2+512,
∴销售单价x=34时,厂商每月能获得最大利润512万元;
(3)当利润为350万元时,-2x2+136x-1800=350,
整理的x2-68x+1075=0,
解得x1=25,x2=43,
∵销售单价不能高于32元,
∴25≤x≤32,
∵销售量y=44-2(x-28)]=-2x+100,
∴y随x的增大而减小,
∴当x=32时,每月的制造成本最低,最低成本=18(-2×32+100)=648万元,
故每月的最低制造成本需要648万元.
∴销售单价每提高1元,销售量相应减少2万件,
∴z=(x-18)[44-2(x-28)]
=(x-18)(100-2x)
=-2x2+136x-1800;
(2)∵z=-2x2+136x-1800=-2(x-34)2+512,
∴销售单价x=34时,厂商每月能获得最大利润512万元;
(3)当利润为350万元时,-2x2+136x-1800=350,
整理的x2-68x+1075=0,
解得x1=25,x2=43,
∵销售单价不能高于32元,
∴25≤x≤32,
∵销售量y=44-2(x-28)]=-2x+100,
∴y随x的增大而减小,
∴当x=32时,每月的制造成本最低,最低成本=18(-2×32+100)=648万元,
故每月的最低制造成本需要648万元.
点评:本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,本题难点在于根据提高的单价表示出销售量.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
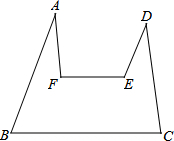 如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.
如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C. 如图,在?ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=
如图,在?ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=