题目内容
7．2014年5月30日，在哈尔滨银泰城中心隆重举行了“哈尔滨市工商联会员联谊会暨六一儿童节木兰希望小学捐赠仪式”，捐赠仪式上木兰教委代表获赠了来自银泰城提供的价值上万元的体育用品，某中学八年级的学生也为木兰希望小学奉献爱心，于是组织了捐款，并用所捐的款项为希望小学的学生们买文具，八年级（1）班和（2）班的班长交流了捐款的情况：八年级（1）班班长说：“我们班捐款总数为1200元，我们班人数比你们班多8人，”八年级（2）班班长说：“我们班捐款总数也为1200元，我们班人均捐款比你们班人均捐款多20%．”（1）求这两个班级每班的人均捐款的钱数；
（2）求这两个班级的总人数．
分析 （1）首先设八年级（1）班的人均捐款数为x元，则八年级（2）班的人均捐款数为（1+20%）x元，然后根据八年级（1）班人数比八年级（2）班多8人，即可得方程：$\frac{1200}{x}$-$\frac{1200}{（1+20%）x}$=8，解此方程即可求得答案．
（2）根据（1）中的每个班级的捐款数计算各种的人数．
解答 解：（1）设八年级（1）班的人均捐款数为x元，则八年级（2）班的人均捐款数为（1+20%）x元，
则：$\frac{1200}{x}$-$\frac{1200}{（1+20%）x}$=8，
解得：x=25，
经检验，x=25是原分式方程的解．
八年级（2）班的人均捐款数为：（1+20%）x=30（元）
答：八年级（1）班人均捐款为25元，八年级（2）班人均捐款为30元．
（2）八年级（1）班的人数：$\frac{1200}{25}$=48（人）．
八年级（2）班人的人数：48-8=40（人）．
则总人数为：48=40=88（人）．
答：这两个班的总人数是88人．
点评 本题考查分式方程的应用．注意分析题意，找到合适的等量关系是解决问题的关键．
练习册系列答案
相关题目
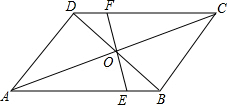如图，在?ABCD中，EF过对角线的交点O，且与边AB、CD分别相交于点E、F、AB=4，AD=3，OF=1.3，求四边形BCFE的周长．
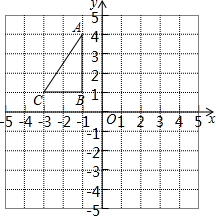如图，在平面直角坐标系中，Rt△ABC的三个顶点均在边长为1的正方形网格格点上．