题目内容
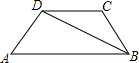 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=4,∠A=60°,BD平分∠ABC,则这个梯形的面积是( )A、6
| ||
B、8
| ||
C、10
| ||
D、12
|
考点:等腰梯形的性质
专题:
分析:过点D作DE⊥AB于E,利用等腰梯形的性质求出DE和AB的长,再利用梯形的面积根据计算即可.
解答:解:过点D作DE⊥AB于E,
∵在等腰梯形ABCD中,AB∥CD,
∴∠A=∠ABC=60°,
∵BD平分∠ABC,
∴∠DBA=30°,
∴∠ADB=90°,
∵AD=BC=4,
∴AB=8,
∴DB=4
,
∴DE=2
,
∴这个梯形的面积是=
(4+4)×2
=8
,
故选B.
∵在等腰梯形ABCD中,AB∥CD,

∴∠A=∠ABC=60°,
∵BD平分∠ABC,
∴∠DBA=30°,
∴∠ADB=90°,
∵AD=BC=4,
∴AB=8,
∴DB=4
| 3 |
∴DE=2
| 3 |
∴这个梯形的面积是=
| 1 |
| 2 |
| 3 |
| 3 |
故选B.
点评:本题考查了等腰梯形的性质,本题涉及到直角三角形的一个定理(直角三角形中30°角所对的直角边等于斜边的一半)以及等腰梯形的性质的运用.

练习册系列答案
相关题目
把(a-1)
中根号外的(a-1)移入根号内得( )
-
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|
某年级学生共有246人,其中男生人数y比女生人数x的2倍少2人,则下面所列的方程组中符合题意的有
( )
( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
下列命题中,假命题的是( )
| A、经过两点有且只有一条直线 |
| B、圆的切线垂直于经过切点的半径 |
| C、两腰相等的梯形叫做等腰梯形 |
| D、平行四边形的对角线相等 |

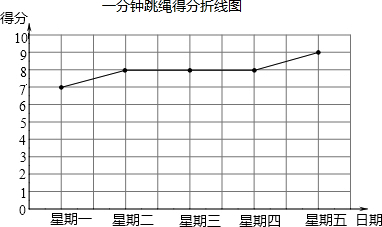 我市体育中考规定:可以在立定跳远和1分钟跳绳中任选一项测试,同学们将根据自己平时的运动成绩确定自己的报考项目,下面是小亮同学在近期的两个项目中连续五次测试的得分情况(立定跳远得分统计表和1分钟跳绳得分折线图).
我市体育中考规定:可以在立定跳远和1分钟跳绳中任选一项测试,同学们将根据自己平时的运动成绩确定自己的报考项目,下面是小亮同学在近期的两个项目中连续五次测试的得分情况(立定跳远得分统计表和1分钟跳绳得分折线图).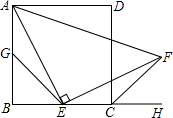 如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.