题目内容
一艘轮船向正西方向航行,在A处测得海岛C在南偏西45°的方向,前进10n mile到达B处,测得海岛C在南偏西30°的方向.若在该海岛方圆5n mile范围内是军事禁区,则该轮船有无闯入禁区的可能?
考点:解直角三角形的应用-方向角问题
专题:
分析:过点C作CD⊥AB于D,则直角△ACD和直角△BCD有公共边CD,在两个直角三角形中,根据公共边CD得到方程,求得CD的长,与5n mile比较,确定轮船继续向正西方向航行,有无闯入禁区的可能.
解答: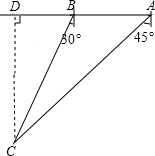 解:如图,过点C作CD⊥AB于D.
解:如图,过点C作CD⊥AB于D.
在直角△ACD中,∠CAD=45°,则直角△ACD是等腰直角三角形,则AD=CD;
在直角△BCD中,∠BCD=30°,则BD=
CD;
∵AB=10n mile,
∴CD-
CD=10,
解得CD=15+5
,
∵15+5
>5,
∴该轮船没有闯入禁区的可能.
 解:如图,过点C作CD⊥AB于D.
解:如图,过点C作CD⊥AB于D.在直角△ACD中,∠CAD=45°,则直角△ACD是等腰直角三角形,则AD=CD;
在直角△BCD中,∠BCD=30°,则BD=
| ||
| 3 |
∵AB=10n mile,
∴CD-
| ||
| 3 |
解得CD=15+5
| 3 |
∵15+5
| 3 |
∴该轮船没有闯入禁区的可能.
点评:本题主要考查了解直角三角形的应用-方向角问题,一般的三角形可以通过作高线转化为解直角三角形的计算,计算时首先计算直角三角形的公共边是常用的思路.

练习册系列答案
相关题目
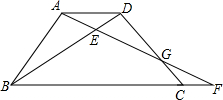 如图,梯形ABCD中,AD∥BC,BC=2AD,点F在BC的延长线上,AF与BD交于点E,AD=2CF,那么△DEG与△CFG的面积比是
如图,梯形ABCD中,AD∥BC,BC=2AD,点F在BC的延长线上,AF与BD交于点E,AD=2CF,那么△DEG与△CFG的面积比是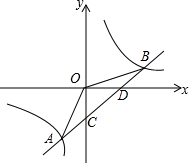 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2= 如图,已知在边长为a的正方形中,剪下一个扇形和一个圆,以此扇形为侧面,圆为底面围成一个圆锥,求此圆锥的表面积.
如图,已知在边长为a的正方形中,剪下一个扇形和一个圆,以此扇形为侧面,圆为底面围成一个圆锥,求此圆锥的表面积.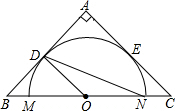 如图,在等腰Rt△ABC中,O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,若OD=3,则AC=
如图,在等腰Rt△ABC中,O为BC的中点,以O为圆心作⊙O交BC于点M、N,⊙O与AB、AC相切,切点分别为D、E,若OD=3,则AC=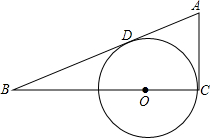 在Rt△ABC中,∠C=90°,AC=3,BC=4,O为BC上一点,以O为圆心,OC为半径作⊙O与AB相切于D,则⊙O的半径为
在Rt△ABC中,∠C=90°,AC=3,BC=4,O为BC上一点,以O为圆心,OC为半径作⊙O与AB相切于D,则⊙O的半径为