题目内容
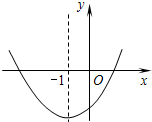二次函数y=mx2+2mx-（3-m）的图象如图所示，则m的取值范围是（ ）| A、m＜3 | B、m＞3 |
| C、m＞0 | D、0＜m＜3 |
考点：二次函数图象与系数的关系
专题：
分析：由抛物线的开口向上知m＞0，由二次函数与y轴交于负半轴可以推出m-3＜0，又抛物线与x轴有两个交点（b2-4ac＞0），可以得到（6-2m）2-4m（m-3）＞0，然后利用前面的结论即可确定m的取值范围．
解答：解：∵抛物线的开口向上，
∴m＞0，①
∵二次函数与y轴交于负半轴，
∴m-3＜0，②
∵抛物线与x轴有两个交点（b2-4ac＞0），
∴（2m）2-4m（m-3）＞0，③，
联立①②③解之得：0＜m＜3．
∴m的取值范围是0＜m＜3．
故选D．
解：∵抛物线的开口向上，∴m＞0，①
∵二次函数与y轴交于负半轴，
∴m-3＜0，②
∵抛物线与x轴有两个交点（b2-4ac＞0），
∴（2m）2-4m（m-3）＞0，③，
联立①②③解之得：0＜m＜3．
∴m的取值范围是0＜m＜3．
故选D．
点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．
练习册系列答案
阅读快车系列答案
相关题目
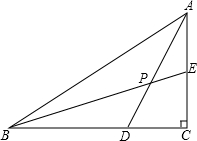如图，在△ABC中，∠C=90°，D、E分别为BC、AC上一点，BD=AC，DC=AE，BE与AD交于点P，则∠ADC+∠BEC=
如图，一次函数y1=kx+b的图象与反比例函数y2=
如图，已知在边长为a的正方形中，剪下一个扇形和一个圆，以此扇形为侧面，圆为底面围成一个圆锥，求此圆锥的表面积．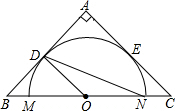
如图，在等腰Rt△ABC中，O为BC的中点，以O为圆心作⊙O交BC于点M、N，⊙O与AB、AC相切，切点分别为D、E，若OD=3，则AC=下列四个数中最小的是（ ）
| A、0 | ||
| B、0.5 | ||
| C、-1 | ||
D、
|
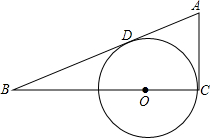在Rt△ABC中，∠C=90°，AC=3，BC=4，O为BC上一点，以O为圆心，OC为半径作⊙O与AB相切于D，则⊙O的半径为多项式4x2+1加上一个数或单项式后，使它称为一个整式的完全平方，那么加上的数或单项式可从①-1②4x③-4x④-4x2中选取（ ）
| A、② | B、③ | C、②③ | D、①②③④ |
下列说法中，正确的有（ ）
①射线与其反向延长线成一条直线；
②直线a，b相交于点m；
③两直线交于两点；
④三条直线两两相交，一定有3个交点．
①射线与其反向延长线成一条直线；
②直线a，b相交于点m；
③两直线交于两点；
④三条直线两两相交，一定有3个交点．
| A、3个 | B、2个 | C、1个 | D、0个 |