题目内容
18.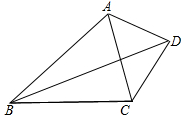 如图,四边形ABCD中,BD平分∠ABC,∠BAC=2∠BDC,若∠BAC=m°,求∠CAD的度数.
如图,四边形ABCD中,BD平分∠ABC,∠BAC=2∠BDC,若∠BAC=m°,求∠CAD的度数.
分析 如图延长BA到M,延长BC到N.设∠DBA=∠DBC=z,∠BAC=n,∠BDC=m,∠ACD=x,∠DCN=y.只要证明x=y,推出CD是∠ACN的外角平分线,由BD平分∠ABC,即可推出AD是∠CAM的平分线,由此即可解决问题.
解答 解:如图延长BA到M,延长BC到N.设∠DBA=∠DBC=z,∠BAC=n,∠BDC=m,∠ACD=x,∠DCN=y.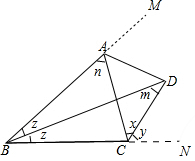
由三角形的外角的性质可知$\left\{\begin{array}{l}{n=2m}&{①}\\{x+y=2z+n}&{②}\\{y=z+m}&{③}\end{array}\right.$
②-③×2得到:x+y-2y=0,
∴x=y,
∴CD是∠ACN的外角平分线,
∵BD平分∠ABC,
∴AD是∠CAM的平分线,
∴∠CAD=$\frac{1}{2}$(180°-∠BAC)=90°-$\frac{1}{2}$m°.
点评 本题考查三角形的外角的性质、角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,学会构建方程组解决问题,题目比较难.

练习册系列答案
相关题目
3.方程x(x-1)=x的解是( )
| A. | x=0 | B. | x=2 | C. | x1=0,x2=1 | D. | x1=0,x2=2 |
7.下列各组中,属于同类项的是( )
| A. | ab与abc | B. | -mn与2mn | C. | 0.5x3y2与2x2y3 | D. | xy2与xz2 |
 如图直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=60°,则∠2=105°.
如图直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=60°,则∠2=105°. 如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=88°,则∠C的度数为46°.
如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=88°,则∠C的度数为46°. 如图,OC平分∠AOB,D为OC上一点,DE⊥OB于E,若DE=5,则D到OA的距离为5.
如图,OC平分∠AOB,D为OC上一点,DE⊥OB于E,若DE=5,则D到OA的距离为5.



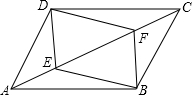 已知:如图,点E和点F是平行四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF.求证:四边形DEBF为平行四边形.
已知:如图,点E和点F是平行四边形ABCD的对角线AC上的两点,AF=CE,连接DE,DF,BE,BF.求证:四边形DEBF为平行四边形.