题目内容
 如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=
如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=| 1 |
| 2 |
(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=
| 1 |
| 2 |
考点:一次函数综合题
专题:综合题
分析:(1)对于直线y=kx+2,令x=0求出y的值,确定出B坐标,得到OB的长,根据OA与OB比值求出OA的长,确定出A坐标,代入直线方程即可求出k的值;
(2)过C作CM垂直于x轴,利用同角的余角相等得到一对角相等,再由一对直角相等,以及AC=AB,利用AAS得到三角形ACM与三角形BAO全等,由全等三角形对应边相等得到CM=OA,AM=OB,由AM+OA求出OM的长,即可确定出C坐标;
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y=
x第一象限上取一点P,连接BP,AP,设点P(m,
m),由三角形ABO面积+三角形BPO面积-三角形AOP面积表示出三角形ABP面积,求出三角形AOB面积,两者相等求出m的值,即可确定出P坐标.
(2)过C作CM垂直于x轴,利用同角的余角相等得到一对角相等,再由一对直角相等,以及AC=AB,利用AAS得到三角形ACM与三角形BAO全等,由全等三角形对应边相等得到CM=OA,AM=OB,由AM+OA求出OM的长,即可确定出C坐标;
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y=
| 1 |
| 2 |
| 1 |
| 2 |
解答: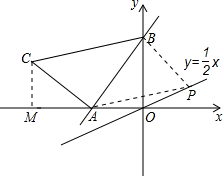 解:(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,
解:(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,
∵OA:OB=
,∴OA=1,即A(-1,0),
将x=-1,y=0代入直线解析式得:0=-k+2,即k=2;
(2)过C作CM⊥x轴,可得∠AMC=∠BOA=90°,
∴∠ACM+∠CAM=90°,
∵△ABC为等腰直角三角形,即∠BAC=90°,AC=BA,
∴∠CAM+∠BAO=90°,
∴∠ACM=∠BAO,
在△CAM和△ABO中,
,
∴△CAM≌△ABO(AAS),
∴AM=OB=2,CM=OA=1,即OM=OA+AM=1+2=3,
∴C(-3,1);
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y=
x第一象限上取一点P,连接BP,AP,
设点P(m,
m),
∴S△ABP=S△ABO+S△BPO-S△AOP=1+m-
m=1+
m,而S△ABC=
AB•AC=
AB2=
(12+22)=
,
可得1+
m=
,
解得:m=2,
则P坐标为(2,1).
 解:(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,
解:(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,∵OA:OB=
| 1 |
| 2 |
将x=-1,y=0代入直线解析式得:0=-k+2,即k=2;
(2)过C作CM⊥x轴,可得∠AMC=∠BOA=90°,
∴∠ACM+∠CAM=90°,
∵△ABC为等腰直角三角形,即∠BAC=90°,AC=BA,
∴∠CAM+∠BAO=90°,
∴∠ACM=∠BAO,
在△CAM和△ABO中,
|
∴△CAM≌△ABO(AAS),
∴AM=OB=2,CM=OA=1,即OM=OA+AM=1+2=3,
∴C(-3,1);
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y=
| 1 |
| 2 |
设点P(m,
| 1 |
| 2 |
∴S△ABP=S△ABO+S△BPO-S△AOP=1+m-
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
可得1+
| 3 |
| 4 |
| 5 |
| 2 |
解得:m=2,
则P坐标为(2,1).
点评:此题属于一次函数综合题,涉及的知识有:坐标与图形性质,全等三角形的判定与性质,一次函数与坐标轴的交点,以及三角形面积求法,熟练掌握一次函数的性质是解本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
一次函数y=kx-b,当k<0,b<0时的图象大致位置是( )
A、 |
B、 |
C、 |
D、 |
下列说法正确的是( )
| A、若x=y,则x2=y2 |
| B、若x2=y2,则x=y |
| C、x2的平方根是x |
| D、x2的算术平方根是x |
下列说法中错误的是 ( )
| A、平行四边形的对角线互相平分 |
| B、菱形的对角线互相垂直平分 |
| C、等腰梯形的对角线相等 |
| D、矩形的对角线互相垂直 |




 如图,有10个城市,分别以点A1,A2,…,A10表示,某人从A1出发,按箭头所指示的方向(不准逆向)可以选择任一路线走向其他某个城市.试求:
如图,有10个城市,分别以点A1,A2,…,A10表示,某人从A1出发,按箭头所指示的方向(不准逆向)可以选择任一路线走向其他某个城市.试求: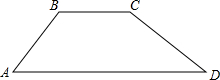 如图,某水库大坝的横截面为梯形ABCD,坝顶宽BC=3米,坝高为2米,背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°.求坝底AD的长度.
如图,某水库大坝的横截面为梯形ABCD,坝顶宽BC=3米,坝高为2米,背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°.求坝底AD的长度.