题目内容
 如图,有10个城市,分别以点A1,A2,…,A10表示,某人从A1出发,按箭头所指示的方向(不准逆向)可以选择任一路线走向其他某个城市.试求:
如图,有10个城市,分别以点A1,A2,…,A10表示,某人从A1出发,按箭头所指示的方向(不准逆向)可以选择任一路线走向其他某个城市.试求:(1)从A1到A5(不绕圈)有多少种走法?
(2)从A1出发按图中所示的方向,绕一圈再回到A1有多少种不同的走法?
考点:推理与论证
专题:
分析:(1)(2)根据已知中有8个城市分别用A1,A2,…,A10表示.某人从A1出发,按箭头所示方向(不可逆行)可以选择任意一条路径走向其他某个城市,那么他从A1出发,按图中所示方向到达A10(每个城市至多经过一次),我们利用分类加法原理,依次计算到达A2,…,A10的走法总数,即可得到答案.
解答:解:(1)由已知中从A1出发,按图中所示方向到达A5(每个城市至多经过一次)
且按箭头所示方向(不可逆行),结合分类加法原理:
则到达A2点共有1种走法;
到达A3点共有1+1=2种走法;
到达A4点共有1+2=3种走法;
到达A5点共有3+2=5种走法;
(2)由(1)得:从A1出发,按图中所示方向到达A10(每个城市至多经过一次)
且按箭头所示方向(不可逆行),结合分类加法原理:
到达A6点共有3+5=8种走法;
到达A7点共有5+8=13种走法;
到达A8点共有8+13=21种走法;
到达A9点共有21+13=34种走法;
到达A10点共有21+34=55种走法;
答:有共55种不同的走法.
且按箭头所示方向(不可逆行),结合分类加法原理:
则到达A2点共有1种走法;
到达A3点共有1+1=2种走法;
到达A4点共有1+2=3种走法;
到达A5点共有3+2=5种走法;
(2)由(1)得:从A1出发,按图中所示方向到达A10(每个城市至多经过一次)
且按箭头所示方向(不可逆行),结合分类加法原理:
到达A6点共有3+5=8种走法;
到达A7点共有5+8=13种走法;
到达A8点共有8+13=21种走法;
到达A9点共有21+13=34种走法;
到达A10点共有21+34=55种走法;
答:有共55种不同的走法.
点评:本题考查了推理与论证,结合分类加法计数原理,在使用分类原理时,分多少类,每一类包含多少种基本事件一定要计算清楚.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知抛物线的解析式为y=
(x-2)2+1,则该抛物线的顶点坐标是( )
| 1 |
| 2 |
| A、(2,1) |
| B、(-2,1) |
| C、(2,-1) |
| D、(1,2) |
 如图.抛物线y=-x2-2x+3与x轴相交于点A和点B,与y轴交于点C.若点P在线段BA上以每秒1个单位长度的速度从点B向点A运动(不与B,A重合),同时,点Q在射线AC上以每秒2个单位长度的速度从A向C运动,则△APQ的面积最大值是( )
如图.抛物线y=-x2-2x+3与x轴相交于点A和点B,与y轴交于点C.若点P在线段BA上以每秒1个单位长度的速度从点B向点A运动(不与B,A重合),同时,点Q在射线AC上以每秒2个单位长度的速度从A向C运动,则△APQ的面积最大值是( ) 如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=
如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB= 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AC、ED的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AC、ED的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.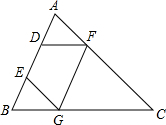 如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,EG∥AC.
如图,D、E是△ABC边AB上的点,F、G分别是边AC、BC上的点,且满足AD=DE=EB,DF∥BC,EG∥AC.
 如图所示,在数轴上有三个点A,B,C,
如图所示,在数轴上有三个点A,B,C,