题目内容
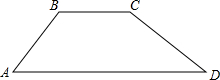 如图,某水库大坝的横截面为梯形ABCD,坝顶宽BC=3米,坝高为2米,背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°.求坝底AD的长度.
如图,某水库大坝的横截面为梯形ABCD,坝顶宽BC=3米,坝高为2米,背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°.求坝底AD的长度.考点:解直角三角形的应用-坡度坡角问题
专题:
分析:首先过B、C作BE⊥AD、CF⊥AD,可得四边形BEFC是矩形,又由背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°,根据坡度的定义,即可求解:
解答: 解:分别过B、C作BE⊥AD、CF⊥AD,垂足为E、F,
解:分别过B、C作BE⊥AD、CF⊥AD,垂足为E、F,
可得:BE∥CF,
又∵BC∥AD,
∴BC=EF BE=CF
由题意,得EF=BC=3,BF=CF=2,
∵背水坡AB的坡度=1:1,
∴∠BAE=45°,
∴AE=BE×cot45°=2×1=2
DF=CF•cot30°=2×
=2
.,
∴AD=AE+EF+DF=2+3+2
=5+2
(米)
答:坝底AD的长度为(5+2
)米.
 解:分别过B、C作BE⊥AD、CF⊥AD,垂足为E、F,
解:分别过B、C作BE⊥AD、CF⊥AD,垂足为E、F,可得:BE∥CF,
又∵BC∥AD,
∴BC=EF BE=CF
由题意,得EF=BC=3,BF=CF=2,
∵背水坡AB的坡度=1:1,
∴∠BAE=45°,
∴AE=BE×cot45°=2×1=2
DF=CF•cot30°=2×
| 3 |
| 3 |
∴AD=AE+EF+DF=2+3+2
| 3 |
| 3 |
答:坝底AD的长度为(5+2
| 3 |
点评:此题考查了坡度坡角问题.此题难度适中,注意构造直角三角形,并借助于解直角三角形的知识求解是关键.

练习册系列答案
相关题目
 如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=
如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=

 如图所示,在数轴上有三个点A,B,C,
如图所示,在数轴上有三个点A,B,C,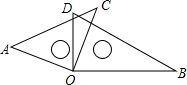 如图,将一副30°和45°的直角三角板的两个直角叠放在一起,使直角顶点重合于点O,若∠AOD=70°,则∠BOC=
如图,将一副30°和45°的直角三角板的两个直角叠放在一起,使直角顶点重合于点O,若∠AOD=70°,则∠BOC=