题目内容
19.已知△ABC的∠A,∠B和∠C的对边分别是a,b和c,下面给出了五组条件:①∠A:∠B:∠C=1:2:3;
②a:b:c=3:4:5;
③2∠A=∠B+∠C;
④a2-b2=c2;
⑤a=6,b=8,c=13.
其中能独立判定△ABC是直角三角形的条件的序号分别是①②④(请写出所有的)
分析 由直角三角形的定义,只要验证最大角是否是90°;由勾股定理的逆定理,只要验证两小边的平方和是否等于最长边的平方即可.
解答 解:①∵∠A:∠B:∠C=1:2:3,∴∠C=$\frac{3}{1+2+3}$×180°=90°,故是直角三角形;
②设a=3k,则b=4k,c=5k,(3k)2+(4k)2=(5k)2,故是直角三角形;
③∵2∠A=∠B+∠C,∠A+∠B+∠C=180°,∴∠A=60°,∠B+∠C=120°,不能判定△ABC是直角三角形;
④∵a2-b2=c2,∴b2+c2=a2,∴是直角三角形;
⑤62+82≠132,∴不能判定△ABC是直角三角形.
能独立判定△ABC是直角三角形的条件的序号分别是①②④.
故答案为:①②④.
点评 本题主要考查三角形内角和,勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
14.一个多边形截取一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
| A. | 5 | B. | 5或6 | C. | 5或7 | D. | 5或6或7 |
4.下列环保标志中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.某班级为筹备新年的联欢会,班长对全班学生爱吃哪几种水果作了民意调查,那么最终买什么水果,下面调查数据中最值得关注的是( )
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 加权平均数 |
 如图:在平面直角坐标系中有△ABC,将△ABC向x轴的负方向平移4个单位得到△A1B1C1,使A点的对应点为A1,B、C的对应点分别为B1、C1.
如图:在平面直角坐标系中有△ABC,将△ABC向x轴的负方向平移4个单位得到△A1B1C1,使A点的对应点为A1,B、C的对应点分别为B1、C1.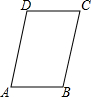 如图,已知四边形ABCD是平行四边形.
如图,已知四边形ABCD是平行四边形.