题目内容
9.菱形的两条对角线长分别为2和2$\sqrt{3}$,则该菱形的高为$\sqrt{3}$.分析 根据对角线的长度即可计算菱形的面积,根据菱形对角线互相垂直平分的性质,可以求得△AOB为直角三角形,根据AO,BO可以求得AB的值,根据菱形的面积和边长即可解题.
解答 解:如图,
由题意知AC=2,BD=2$\sqrt{3}$,
则菱形的面积S=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∵菱形对角线互相垂直平分,
∴△AOB为直角三角形,AO=1,BO=$\sqrt{3}$,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=2,
∴菱形的高h=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了勾股定理在直角三角形中的运用,菱形面积的计算,本题中求根据AO,BO的值求AB是解题的关键.

练习册系列答案
相关题目
20.小芳家房屋装修时,选中了一种漂亮的正八边形地砖.建材店老板告诉她,只用一种八边形地砖是不能密铺地面的,便向她推荐了几种形状的地砖.你认为要使地面密铺,小芳应选择另一种形状的地砖是( )
| A. | 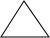 | B. |  | C. | 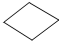 | D. | 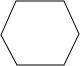 |
1.有一个多边形,它的内角和恰好等于它的外角和的2倍,则这个多边形的边数是( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
18.若y=kx+2的函数值y随着x的增大而增大,则k的值可能是( )
| A. | 0 | B. | 1 | C. | -30 | D. | -2 |
19. 如图,描述了安佶同学某日造成的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后:马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示安佶离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )
如图,描述了安佶同学某日造成的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后:马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示安佶离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )
 如图,描述了安佶同学某日造成的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后:马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示安佶离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )
如图,描述了安佶同学某日造成的一段生活过程:他早上从家里跑步去书店,在书店买了一本书后:马上就去早餐店吃早餐,吃完早餐后,立即散步走回家.图象中的平面直角坐标系中的x表示时间,y表示安佶离家的距离.请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )| A. | 安佶从家到新华书店的平均速度是10千米/分钟 | |
| B. | 安佶买书花了15分钟 | |
| C. | 安佶吃早餐花了20分钟 | |
| D. | 从早餐店到安佶家的1.5千米 |