题目内容
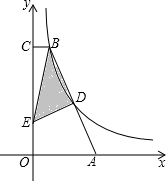 如图,B、D两点均在双曲线y=
如图,B、D两点均在双曲线y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:连结AE,过B、D分别作BF⊥AO,DM⊥AO,根据点D为AB的中点,△BDE的面积为7可得△AEB的面积为14,设B点坐标为(a,b),再证明△ADM∽△ABF可得FM=AM,进而表示出EO=
b,CE=
b,AO=3a,再根据S梯形OABC=S△CBE+S△EBA+S△OEA,进行计算即可.
| 1 |
| 3 |
| 2 |
| 3 |
解答:解:连结AE,过B、D分别作BF⊥AO,DM⊥AO,如图,
∵点D为AB的中点,△BDE的面积为7,
∴△ADE的面积为7,
∴△AEB的面积为14,
设B点坐标为(a,b),
∵点D为AB的中点,
∴D点纵坐标为
b,
∵B、D两点均在双曲线y=
上,
∴D点横坐标为2a,
∴D(2a,
b),
∵BF⊥AO,DM⊥AO,
∴FB∥DM,
∴△ADM∽△ABF,
∴
=
=
,
∴FM=MA=a,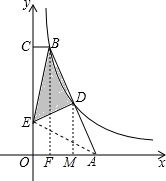
∴A(3a,0),
∵B点坐标为(a,b),
则CB=a,OC=b,
∵CE=2OE,
∴EO=
b,CE=
b,
∵S梯形OABC=S△CBE+S△EBA+S△OEA,
∴
×(a+3a)×b=
×a×
b+14+
×
b×3a,
解得:ab=12,
∵B在双曲线y=
上,
∴k=12,
故答案为:12.
∵点D为AB的中点,△BDE的面积为7,
∴△ADE的面积为7,
∴△AEB的面积为14,
设B点坐标为(a,b),
∵点D为AB的中点,
∴D点纵坐标为
| 1 |
| 2 |
∵B、D两点均在双曲线y=
| k |
| x |
∴D点横坐标为2a,
∴D(2a,
| 1 |
| 2 |
∵BF⊥AO,DM⊥AO,
∴FB∥DM,
∴△ADM∽△ABF,
∴
| AM |
| AF |
| AD |
| AB |
| 1 |
| 2 |
∴FM=MA=a,

∴A(3a,0),
∵B点坐标为(a,b),
则CB=a,OC=b,
∵CE=2OE,
∴EO=
| 1 |
| 3 |
| 2 |
| 3 |
∵S梯形OABC=S△CBE+S△EBA+S△OEA,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解得:ab=12,
∵B在双曲线y=
| k |
| x |
∴k=12,
故答案为:12.
点评:此题主要考查了反比例函数 图象上点的坐标特点,关键是正确找到AO和CB的关系.

练习册系列答案
相关题目
若一个正多边形的一个外角为60°,则它的内切圆半径与外接圆半径之比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各数中,最大的数是( )
A、
| ||
| B、0 | ||
| C、|-4| | ||
| D、π |
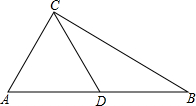 在Rt△ABC中,∠C=90°,BC=2
在Rt△ABC中,∠C=90°,BC=2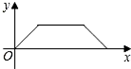 如图所示是李老师早晨出门散步时,离家的距离y与时间x之间的函数图象,若用黑点表示李老师家的位置,则李老师散步行走的路线可能是( )
如图所示是李老师早晨出门散步时,离家的距离y与时间x之间的函数图象,若用黑点表示李老师家的位置,则李老师散步行走的路线可能是( )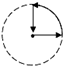
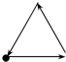
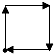

 在Rt△ABC中,∠C=90°,BC=
在Rt△ABC中,∠C=90°,BC=