题目内容
设x1、x2是方程x2+x-3=0的两根,那么x13-4x22+20= .
考点:根与系数的关系,代数式求值
专题:计算题
分析:先根据x1、x2是方程x2+x-3=0的两根,把x1、x2代入此方程可得x12+x1-3=0,x22+x2-3=0,即x12=3-x1,x22=3-x2,由根与系数的关系得,x1+x2=-1,x1•x2=-3,再把此关系代入x13-4x22+20进行计算即可.
解答:解:∵x1、x2是方程x2+x-3=0的两根,
∴x12+x1-3=0,x22+x2-3=0,即x12=3-x1…①,x22=3-x2…②,x1+x2=-1…③,x1•x2=-3,
∴x13-4x22+20
=x1•x12-4x22+20
=x1•(3-x1)-4(3-x2)+20
=3x1-x12-12+4x2+20
=3x1-(3-x1)-12+4x2+20
=4(x1+x2)-3-12+20
=-4-3-12+20
=1.
故答案为:1.
∴x12+x1-3=0,x22+x2-3=0,即x12=3-x1…①,x22=3-x2…②,x1+x2=-1…③,x1•x2=-3,
∴x13-4x22+20
=x1•x12-4x22+20
=x1•(3-x1)-4(3-x2)+20
=3x1-x12-12+4x2+20
=3x1-(3-x1)-12+4x2+20
=4(x1+x2)-3-12+20
=-4-3-12+20
=1.
故答案为:1.
点评:本题考查的是一元二次方程根与系数的关系及代数式求值,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
已知
=
=
,且a,b,c互不相等,则x+y+z等于( )
| a-b |
| x |
| b-c |
| y |
| c-a |
| z |
| A、a+b-c | ||
| B、0 | ||
C、
| ||
| D、1 |
(x+a)(x+b)+(x+b)(x+c)+(x+c)(x+a)是完全平方式,则a,b,c的关系可以写成( )
| A、a<b<c |
| B、(a-b)2+(b-c)2=0 |
| C、c<a<b |
| D、a=b≠c |
下列图形中,不是轴对称图形的是( )
| A、直角三角形ABC |
| B、角DOE |
| C、等边三角形FGH |
| D、线段MN |
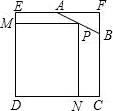 如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )
如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( ) 要挖一个面积为432m2的矩形养鱼池,周围两侧分别有宽为3m和4m的堤堰,如图所示,要想占地总面积最少,问水池的长与宽应为多少?
要挖一个面积为432m2的矩形养鱼池,周围两侧分别有宽为3m和4m的堤堰,如图所示,要想占地总面积最少,问水池的长与宽应为多少?