题目内容
20.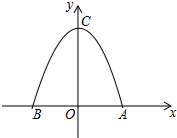 某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2.
某菜农搭建了一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,抛物线的表达式为y=-$\frac{1}{2}$x2+2.(1)若菜农的身高是1.60米,他在不弯腰的情况下,横向活动的范围是几米?(精确到0.01米)
(2)大棚的宽度是多少?
(3)大棚的最高点离地面几米?
分析 (1)根据题意求出y=1.6时x的值,进而求出答案;
(2)根据题意求出y=0时x的值,进而求出答案;
(3)直接求出函数最值即可.
解答 解:(1)∵抛物线的大棚函数表达式为y=-$\frac{1}{2}$x2+2,
∴菜农的身高为1.6m,即y=1.6,
则1.6=-$\frac{1}{2}$x2+2,
解得x≈±0.894.
故菜农的横向活动的范围是0.894-(-0.894)=1.788≈1.79(米);
(2)当y=0则,0=-$\frac{1}{2}$x2+2,
解得:x1=2,x2=-2,
则AB=2×2=4米,
所以大棚的宽度是4m;
(3)当x=0时,y最大=2,
即大棚的最高点离地面2米.
点评 此题主要考查了二次函数应用以及一元二次方程的解法,正确理解方程与函数关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列各点中,在函数y=$\frac{2}{x}$的图象上的点是( )
| A. | (1,0.5) | B. | (2,-1) | C. | (-1,-2) | D. | (-2,1) |
15. 如图所示几何体三视图的主视图是( )
如图所示几何体三视图的主视图是( )
 如图所示几何体三视图的主视图是( )
如图所示几何体三视图的主视图是( )| A. |  | B. |  | C. |  | D. |  |
5.下列说法正确的有( )
①2的相反数是±2;
②相等的角叫对顶角;
③两点之间的所有连线中,线段最短;
④过一点有且只有一条直线与已知直线垂直;
⑤立方等于它本身的数有0和±1
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
①2的相反数是±2;
②相等的角叫对顶角;
③两点之间的所有连线中,线段最短;
④过一点有且只有一条直线与已知直线垂直;
⑤立方等于它本身的数有0和±1
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列方程是一元二次方程的是( )
| A. | x2-6x+2 | B. | 2x2-y+1=0 | C. | 5x2=0 | D. | $\frac{1}{{x}^{2}}$+x=2 |
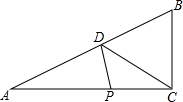 在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )
在Rt△ABC中,∠ACB=90°,点D是斜边AB上的中点,AC=6cm,BC=4cm,一动点P从点A出发,沿A→C→B的路线以1cm/s的速度移动.设△APD的面积为y(cm2),则y关于点P的运动时间x(s)的函数图象大致是( )



 一个几何体由12个大小相同的小立方体搭成,从上面看到的这个几何体的形状图如图所示,若小正方形中的数字表示在该位置小立方块的个数,则从正面看,一共能看到8个小立方块(被遮挡的不计).
一个几何体由12个大小相同的小立方体搭成,从上面看到的这个几何体的形状图如图所示,若小正方形中的数字表示在该位置小立方块的个数,则从正面看,一共能看到8个小立方块(被遮挡的不计).