题目内容
 已知,如图,CD是Rt△ABC斜边上的中线,DE⊥AB交BC于F,交AC的延长线于E,求证:
已知,如图,CD是Rt△ABC斜边上的中线,DE⊥AB交BC于F,交AC的延长线于E,求证:(1)△ADE∽△FDB;
(2)CD2=DE•DF.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)利用∠ACE=∠EDB和∠DBF=∠CEF,即可得出△ADE∽△FDB;
(2)由△ADE∽△FDB,可得
=
,再由CD是Rt△ABC斜边上的中线,得出DA=DB=CD,即可得出CD2=DE•DF.
(2)由△ADE∽△FDB,可得
| DE |
| DB |
| DA |
| DF |
解答:解:(1)∵DE⊥AB,△ABC是RT△,
∴∠ACB=∠EDB=90°,
∵∠DFB=∠CFE,
∴∠DBF=∠CEF,
∴△ADE∽△FDB;
(2)∵△ADE∽△FDB,
∴
=
∵CD是Rt△ABC斜边上的中线,
∴DA=DB=CD,
∴
=
,
∴CD2=DE•DF.
∴∠ACB=∠EDB=90°,
∵∠DFB=∠CFE,
∴∠DBF=∠CEF,
∴△ADE∽△FDB;
(2)∵△ADE∽△FDB,
∴
| DE |
| DB |
| DA |
| DF |
∵CD是Rt△ABC斜边上的中线,
∴DA=DB=CD,
∴
| DE |
| CD |
| CD |
| DF |
∴CD2=DE•DF.
点评:本题主要考查了相似三角形的判定与性质,解题的关键是运用直角三角形斜边中线的性质.

练习册系列答案
相关题目
 在△ABC中,设D是BC边上的中点,DE平分∠ADB交AB于点E,DF平分∠ADC交AC于点F,则EF与BE+CF的关系是( )
在△ABC中,设D是BC边上的中点,DE平分∠ADB交AB于点E,DF平分∠ADC交AC于点F,则EF与BE+CF的关系是( )| A、BE+CF=EF |
| B、BE+CF>EF |
| C、BE+CF<EF |
| D、不能确定 |
 函数y=x与y=
函数y=x与y=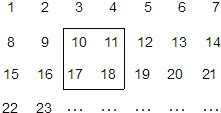 把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表.
把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表. 已知:如图,线段a,
已知:如图,线段a,
