题目内容
16.观察下列一组等式,然后解答后面的问题:($\sqrt{2}$+1)($\sqrt{2}$-1)=1,($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$$-\sqrt{2}$)=1,($\sqrt{4}$+$\sqrt{3}$)($\sqrt{4}$-$\sqrt{3}$)=1,($\sqrt{5}$+$\sqrt{4}$)($\sqrt{5}$-$\sqrt{4}$)=1,…(1)观察上面的规律,计算下列式子的值.
($\frac{1}{\sqrt{2}+1}$$+\frac{1}{\sqrt{3}+\sqrt{2}}$$+\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$)($\sqrt{2016}$+1)
(2)利用上面的规律,试比较$\sqrt{12}$-$\sqrt{11}$与$\sqrt{13}$-$\sqrt{12}$的大小.
分析 (1)根据分母乘以分母中这两个数的差,可分母有理化,根据实数的运算,可得答案;
(2)根据平方差公式,可化成分子相同的数,根据相同的分子,分母越大的数越小,可得答案.
解答 解:(1)原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)=($\sqrt{2016}$+1)($\sqrt{2016}$-1)=2016-1=2015;
(2)$\sqrt{12}$-$\sqrt{11}$=$\frac{(\sqrt{12}-\sqrt{11})(\sqrt{12}+\sqrt{11})}{\sqrt{12}+\sqrt{11}}$=$\frac{12-11}{\sqrt{12}+\sqrt{11}}$=$\frac{1}{\sqrt{12}+\sqrt{11}}$,
$\sqrt{13}$-$\sqrt{12}$=$\frac{(\sqrt{13}-\sqrt{12})(\sqrt{13}+\sqrt{12})}{\sqrt{13}+\sqrt{12}}$=$\frac{13-12}{\sqrt{13}+\sqrt{12}}$=$\frac{1}{\sqrt{13}+\sqrt{12}}$,
$\sqrt{12}$-$\sqrt{11}$>$\sqrt{13}$-$\sqrt{12}$.
点评 本题考查了分母有理化,利用平方差公式是分母有理化的方法.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.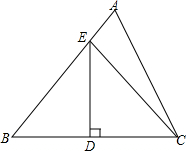 如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )
如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )
 如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )
如图,在△ABC中,D是BC边的中点,过D作BC的垂线,交AB于点E,已知BD=5,CE=8,那么△BCE的周长为( )| A. | 18 | B. | 20 | C. | 26 | D. | 28 |
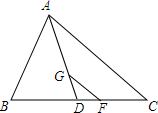 如图ABC中,G是重心,AG的延长线交BC于D,过点G作GF∥AC,交BC于F,则S△DGF:S△DAC=1:9.
如图ABC中,G是重心,AG的延长线交BC于D,过点G作GF∥AC,交BC于F,则S△DGF:S△DAC=1:9.