题目内容
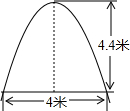 某工厂大门是抛物线形水泥建筑,大门地面宽为4m,顶部距离地面的高度为4.4m,
某工厂大门是抛物线形水泥建筑,大门地面宽为4m,顶部距离地面的高度为4.4m,现有一辆满载货物的汽车欲通大门,其装货宽度为2.4m,该车要想过此门,装货后
的最大高度应是
考点:二次函数的应用
专题:
分析:首先建立适当的平面直角坐标系并利用图象中的数据确定二次函数的解析式,然后代入x=1.2确定OB的长度,从而确定汽车的最大高度.
解答: 解:建立如图平面直角坐标系:
解:建立如图平面直角坐标系:
设抛物线的解析式为y=ax2,
由题意得:点A的坐标为(2,-4.4),
∴-4.4=4a,
解得:a=-1.1,
∴抛物线的解析式为y=-1.1x2,
当x=1.2时,
y=-1.1×1.44=-1.584,
∴线段OB的长为1.584米,
∴BC=4.4-1.584=2.816米,
∴装货后的最大高度为2.816米,
故答案为:2.816米.
 解:建立如图平面直角坐标系:
解:建立如图平面直角坐标系:设抛物线的解析式为y=ax2,
由题意得:点A的坐标为(2,-4.4),
∴-4.4=4a,
解得:a=-1.1,
∴抛物线的解析式为y=-1.1x2,
当x=1.2时,
y=-1.1×1.44=-1.584,
∴线段OB的长为1.584米,
∴BC=4.4-1.584=2.816米,
∴装货后的最大高度为2.816米,
故答案为:2.816米.
点评:本题考查点的坐标的求法及二次函数的实际应用关键是建立数学模型,借助二次函数解决实际问题,注意根据线段长度得出各点的坐标,难度一般.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
下列说法中正确的是( )
| A、数轴上距离原点2个单位长度的点表示的数是2 |
| B、-1是最大的负整数 |
| C、任何有理数的绝对值都大于0 |
| D、0是最小的有理数 |
 如图,有背面一样,正面分别是2、3、4、5的4张扑克牌,两次随机摸一张牌看正面的点数(每一次摸牌后放回)
如图,有背面一样,正面分别是2、3、4、5的4张扑克牌,两次随机摸一张牌看正面的点数(每一次摸牌后放回) 把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP=
把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP= 一只蚂蚁从长为4cm,高时5cm的长方体纸箱的A点沿纸箱跑到B点,有不同的爬行路线.画出平面图示(相同类型画一个),并通过计算说明哪条线路最短,最短路线长多少?
一只蚂蚁从长为4cm,高时5cm的长方体纸箱的A点沿纸箱跑到B点,有不同的爬行路线.画出平面图示(相同类型画一个),并通过计算说明哪条线路最短,最短路线长多少?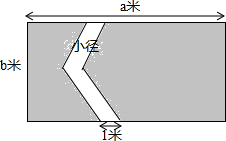 如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积.
如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积.