题目内容
1.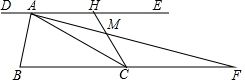 如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=$\frac{1}{3}$AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是$\frac{1}{12}$,则$\frac{1}{tan∠ACH}$的值是8-$\sqrt{15}$.
如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=$\frac{1}{3}$AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是$\frac{1}{12}$,则$\frac{1}{tan∠ACH}$的值是8-$\sqrt{15}$.
分析 过点H作HG⊥AC于点G,由于AF平分∠CAE,DE∥BF,∠HAF=∠AFC=∠CAF,从而AC=CF=2,利用△AHM∽△FCM,$\frac{AM}{MF}$=$\frac{AH}{CF}$,从而可求出AH=1,利用△AMH的面积是$\frac{1}{12}$,从而可求出HG,利用勾股定理即可求出CG的长度,所以$\frac{1}{tan∠ACH}$=$\frac{CG}{HG}$.
解答 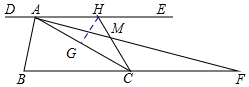 解:过点H作HG⊥AC于点G,
解:过点H作HG⊥AC于点G,
∵AF平分∠CAE,DE∥BF,
∴∠HAF=∠AFC=∠CAF,
∴AC=CF=2,
∵AM=$\frac{1}{3}$AF,
∴$\frac{AM}{MF}$=$\frac{1}{2}$,
∵DE∥CF,
∴△AHM∽△FCM,
∴$\frac{AM}{MF}$=$\frac{AH}{CF}$,
∴AH=1,
设△AHM中,AH边上的高为m,
△FCM中CF边上的高为n,
∴$\frac{m}{n}$=$\frac{AM}{MF}$=$\frac{1}{2}$,
∵△AMH的面积为:$\frac{1}{12}$,
∴$\frac{1}{12}$=$\frac{1}{2}$AH•m
∴m=$\frac{1}{6}$,
∴n=$\frac{1}{3}$,
设△AHC的面积为S,
∴$\frac{S}{{S}_{△AHM}}$=$\frac{m+n}{m}$=3,
∴S=3S△AHM=$\frac{1}{4}$,
∴$\frac{1}{2}$AC•HG=$\frac{1}{4}$,
∴HG=$\frac{1}{4}$,
∴由勾股定理可知:AG=$\frac{\sqrt{15}}{4}$,
∴CG=AC-AG=2-$\frac{\sqrt{15}}{4}$
∴$\frac{1}{tan∠ACH}$=$\frac{CG}{HG}$=8-$\sqrt{15}$
故答案为:8-$\sqrt{15}$
点评 本题考查相似三角形综合问题,解题的关键是通过相似三角形的性质求出HG、CG、AH长度,本题属于难题.


| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |

| A. | 甲正确,乙错误 | B. | 乙正确,甲错误 | C. | 甲、乙均正确 | D. | 甲、乙均错误 |
| A. | 0.826×106 | B. | 8.26×107 | C. | 82.6×106 | D. | 8.26×108 |
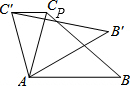 如图,在△ABC中,∠CAB=78°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,BC与B′C′交于点P,则∠BPB′的大小为24°.
如图,在△ABC中,∠CAB=78°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,BC与B′C′交于点P,则∠BPB′的大小为24°. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.