题目内容
5.求不等式组$\left\{\begin{array}{l}{\frac{4(1+x)}{3}-1≤\frac{5+x}{2}…①}\\{x-5≤\frac{3}{2}(3x-2)…②}\end{array}\right.$的整数解.分析 先求出不等式的解,然后根据大大取大,小小取小,大小小大中间找,大大小小解不了,的口诀求出不等式组的解,进而求出整数解.
解答 解:解不等式①得x≤$\frac{13}{5}$,
解不等式②得x≥-$\frac{4}{7}$,
∴不等式组的解集为:-$\frac{4}{7}$≤x≤$\frac{13}{5}$
∴不等式组的整数解是0,1,2.
点评 本题考查不等式组的解法,关键是求出不等式的解,然后根据口诀求出不等式组的解,再求出整数解.

练习册系列答案
相关题目
15.学校最近新配备了一批图书需要甲乙两人进行整理,若甲单独整理完成需要4小时完工;若甲乙共同整理2小时后,乙再单独整理2小时才能完工,则乙单独整理完成需要( )
| A. | 4小时 | B. | 6小时 | C. | 8小时 | D. | 10小时 |
16.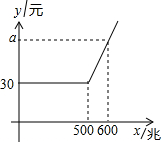 如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )
如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )
 如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )
如图是某通讯公司的4G上网套餐每月上网费用y(单位:元)与上网流量x(单位;兆)之间函数关系的图象.若该公司每户每月上网流量超过500兆以后,每兆流量需加收0.29元.则图中a的值为( )| A. | 140 | B. | 174 | C. | 59 | D. | 69 |
20.下列说法中,正确的是( )
| A. | 将一组数据中的每一个数据都加同一个正数,方差变大 | |
| B. | 为了解全市同学对书法课的喜欢情况,调查了某校所有女生 | |
| C. | “任意画出一个矩形,它是轴对称图形”是必然事件 | |
| D. | 为了审核书稿中的错别字,选择抽样调查 |
14. 有一个外包装盒为正六棱柱体(如图),它的左视图是( )
有一个外包装盒为正六棱柱体(如图),它的左视图是( )
 有一个外包装盒为正六棱柱体(如图),它的左视图是( )
有一个外包装盒为正六棱柱体(如图),它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
15.下列四个数中,最小的数是( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 3 |
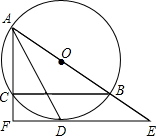 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的直线分别交AB,AC的延长线于点E,F,AF⊥EF.