题目内容
 如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,10时到达B处,从A处测得灯塔C在北偏西30°方向,从B处测得灯塔C在北偏西60°方向,则A处到灯塔C的距离是
如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,10时到达B处,从A处测得灯塔C在北偏西30°方向,从B处测得灯塔C在北偏西60°方向,则A处到灯塔C的距离是考点:勾股定理的应用,方向角
专题:
分析:先过点C作CD⊥AB于点D,再根据三角形外角的性质可求得BC的值,然后放到Rt△BCD中,借助60°角的正弦值即可解答.
解答: 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
∵∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
∴BC=BA=30海里,
∵∠CDB=90°,
∴sin∠CBD=
.
∴sin60°=
=
.
∴CD=BC×
=30×
=15
(海里),
∴AC=2CD=30
(海里).
∴此时轮船与灯塔C的距离为30
海里.
故答案为:30
.
 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,∵∠CAB=30°,∠CBD=60°,
∴∠ACB=30°,
∴BC=BA=30海里,
∵∠CDB=90°,
∴sin∠CBD=
| CD |
| BC |
∴sin60°=
| CD |
| BC |
| ||
| 2 |
∴CD=BC×
| ||
| 2 |
| ||
| 2 |
| 3 |
∴AC=2CD=30
| 3 |
∴此时轮船与灯塔C的距离为30
| 3 |
故答案为:30
| 3 |
点评:本题考查的是勾股定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
在数2,
,-3.14,
,0.2,0.
,5.1010010001中,其中无理数有( )
| π |
| 3 |
| 22 |
| 7 |
| • |
| 2 |
| • |
| 3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
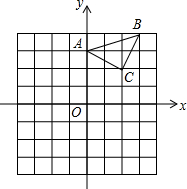 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)请以点B为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,并求出△A1B1C1的面积.
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)请以点B为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,并求出△A1B1C1的面积. 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,BC=8.求△ADE周长.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,BC=8.求△ADE周长. 下图是由八块积木搭成,这几块积木都是相同的正方体,请画出这个图形的主视图、左视图和俯视图.
下图是由八块积木搭成,这几块积木都是相同的正方体,请画出这个图形的主视图、左视图和俯视图.