题目内容
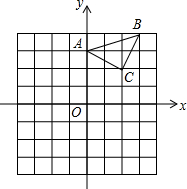 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)请以点B为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,并求出△A1B1C1的面积.
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)请以点B为位似中心,在网格中画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,并求出△A1B1C1的面积.考点:作图-位似变换
专题:
分析:利用位似图形的性质得出对应点位置进而利用矩形面积减去周围三角形面积进而得出答案.
解答: 解:如图所示:△A1B1C1即为所求,
解:如图所示:△A1B1C1即为所求,
△A1B1C1的面积为:4×6-
×2×6-
×2×4-
×2×4=10.
 解:如图所示:△A1B1C1即为所求,
解:如图所示:△A1B1C1即为所求,△A1B1C1的面积为:4×6-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了位似图形的画法以及三角形面积求法,得出对应点位置是解题关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
某商场经销一批空调,进价为每台x元,原零售价比进价高m%,后根据市场变化,把零售价调整为原零售价的n%,则调整后的零售价为每台( )
| A、(1+m%•n%)x元 |
| B、(1+m%)n%•x元 |
| C、(1+m%)(1-n%)x元 |
| D、m%(1-n%)x元 |
 如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,10时到达B处,从A处测得灯塔C在北偏西30°方向,从B处测得灯塔C在北偏西60°方向,则A处到灯塔C的距离是
如图,上午8时,一艘船从A处出发,以15海里/时的速度向正北方向航行,10时到达B处,从A处测得灯塔C在北偏西30°方向,从B处测得灯塔C在北偏西60°方向,则A处到灯塔C的距离是