题目内容
7.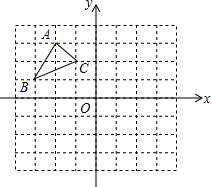 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.(1)写出A、C的坐标;
(2)画出△ABC绕点B顺时针旋转90°得△A1BC1;
(3)求出(2)旋转过程中点A所经过的路径长.(结果保留π)
分析 (1)根据第二象限点的坐标特征写出A、C的坐标;
(2)利用网格特点和旋转的性质,画出点A、C的对应点A1、C1即可得到△A1BC1;
(3)先利用勾股定理计算出BA,由于点A到点A1经过路径是以点B为圆心,BA为半径,圆心角为90°的弧,于是根据弧长公式可计算出点A到点A1经过的路径的长.
解答 解:(1)A点坐标为(2,3),C点坐标为(-1,2);
(2)如图,△A1BC1为所作;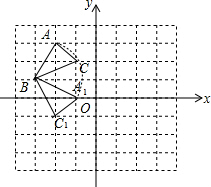
(3)BA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
所以点A所经过的路径长=$\frac{90•π•\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π.
点评 本题考查了作图-旋转变换法:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
也考查了弧长公式.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
17.在5,$\sqrt{6}$,π,-3,$\frac{3}{4}$,3.14,0.010010001…,$\frac{22}{27}$,$\frac{π}{2}$九个数中,无理数的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
2.边心距为2的等边三角形边长是( )
| A. | 4 | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2 |
12.若x2+(m-3)x+16是完全平方式,则m的值是( )
| A. | 11 | B. | -5 | C. | ±8 | D. | 11或-5 |
19. 用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )
用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )
 用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )
用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
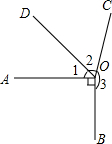 (1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
(1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?