Question

3．在⊙O中，OC是半径，弦EF过OC的中点且垂直于OC，则弦EF所对的圆心角的度数是120°，弦EF的弦心距和弦EF的长的比是$\sqrt{3}$：6．

Answer 1

分析 连接OE，OF，根据直角三角形的性质得到∠OEA=30°，求出∠EOF的度数，设OA=x，根据勾股定理表示出EF，求比即可．

解答 解：连接OE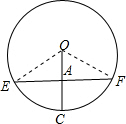，OF，
∵OA=$\frac{1}{2}$OC，
∴OA=$\frac{1}{2}$OE，又OC⊥EF，
∴∠OEA=30°，
∴∠EOA=60°，
∴∠EOF=120°，
设OA=x，则OE=2x，
由勾股定理得，AE=$\sqrt{3}$x，则EF=2$\sqrt{3}$x，
∴OA：EF=$\sqrt{3}$：6，
故答案为：120°；$\sqrt{3}$：6．

点评 本题考查的是垂径定理和勾股定理的应用，在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．