题目内容
15.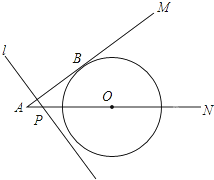 如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是$\frac{5}{4}$或$\frac{35}{4}$秒.
如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是$\frac{5}{4}$或$\frac{35}{4}$秒.
分析 当l平移到l′和l″时,与⊙O相切,切点分别为C点和D点,如图,根据切线的性质得到四边形BOCE和四边形BODF都是矩形,则BE=OC=6,BF=OD=6,在Rt△AOB中利用勾股定理计算出AB=8,则AE=AB-BE=2,AF=AB+BF=14,利用PE∥OB得到$\frac{AP}{AO}=\frac{AE}{AB}$,利用比例性质可计算出AP=$\frac{5}{2}$,易得点P运动的时间为$\frac{5}{4}$秒;接着证明△QOD∽△QAF,利用相似比计算出AQ=$\frac{35}{2}$,易得点P运动到点Q时的时间为$\frac{35}{4}$秒.
解答 解: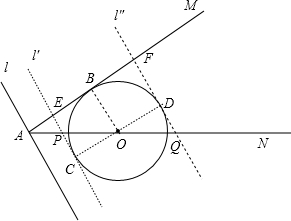 当l平移到l′和l″时,与⊙O相切,切点分别为C点和D点,如图,
当l平移到l′和l″时,与⊙O相切,切点分别为C点和D点,如图,
则OC=OD=6,OC⊥l′,OD⊥l″,
∵⊙O与射线AM相切于点B,
∴OB⊥AM,
∵l⊥AB,
∴四边形BOCE和四边形BODF都是矩形,
∴BE=OC=6,BF=OD=6,
在Rt△AOB中,∵OB=6,OA=10,
∴AB=$\sqrt{O{A}^{2}-O{B}^{2}}$=8,
∴AE=AB-BE=2,AF=AB+BF=14,
∵PE∥OB,
∴$\frac{AP}{AO}=\frac{AE}{AB}$,即$\frac{AP}{10}=\frac{2}{8}$,
∴AP=$\frac{5}{2}$,
∴点P运动的时间=$\frac{5}{2}$÷2=$\frac{5}{4}$(秒);
∵OD∥AF,
∴△QOD∽△QAF,
∴$\frac{OQ}{AQ}=\frac{OD}{AF}$,即$\frac{AQ-10}{AQ}=\frac{6}{14}$,
∴AQ=$\frac{35}{2}$,
∴点P运动到点Q时的时间=$\frac{35}{2}$÷2=$\frac{35}{4}$(秒),
即当l与⊙O相切时,所用时间为$\frac{5}{4}$秒或$\frac{35}{4}$秒.
故答案为:$\frac{5}{4}$或$\frac{35}{4}$.
点评 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了矩形的性质和相似三角形的判定与性质.

| A. |  | B. |  | C. |  | D. |  |
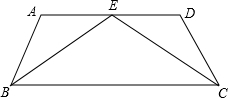 如图,AD∥BC,∠A=94°,∠D=106°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.
如图,AD∥BC,∠A=94°,∠D=106°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.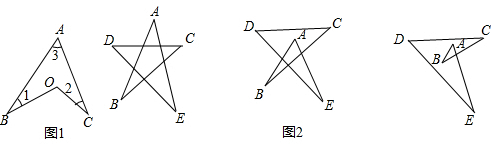
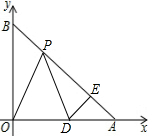 已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
已知在平面直角坐标系中,A(a、o)、B(o、b)满足$\sqrt{a-b}$+|a-3$\sqrt{2}$|=0,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.