题目内容
5.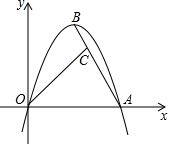 已知二次函数y=ax2+2$\sqrt{3}$x(a<0)的图象与x轴交于A(6,0),顶点为B,C为线段AB上一点,BC=2,D为x轴上一动点.若BD=OC,则D的坐标为D(2,0)或(4,0).
已知二次函数y=ax2+2$\sqrt{3}$x(a<0)的图象与x轴交于A(6,0),顶点为B,C为线段AB上一点,BC=2,D为x轴上一动点.若BD=OC,则D的坐标为D(2,0)或(4,0).
分析 把A(6,0)代入y=ax2+2$\sqrt{3}$x得0=62a+2$\sqrt{3}$×6,得到y=-$\frac{\sqrt{3}}{3}$x2+2$\sqrt{3}$x,根据抛物线的顶点坐标公式得到B(3,3$\sqrt{3}$),根据两点间的距离公式得到AB=$\sqrt{(6-3)^{2}+(3\sqrt{3})^{2}}$=6,过B作BE⊥OA于E,CF⊥OA与F,根据相似三角形的性质得到AF=2,CF=2$\sqrt{3}$,根据两点间的距离公式得到OC=$\sqrt{C{F}^{2}+O{F}^{2}}$=2$\sqrt{7}$,根据BD=OC,列方程即可得到结论.
解答 解:把A(6,0)代入y=ax2+2$\sqrt{3}$x得0=62a+2$\sqrt{3}$×6,
∴a=-$\frac{\sqrt{3}}{3}$,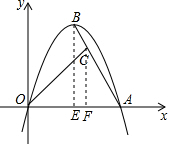
∴y=-$\frac{\sqrt{3}}{3}$x2+2$\sqrt{3}$x,
∵顶点为B,
∴B(3,3$\sqrt{3}$),
∴AB=$\sqrt{(6-3)^{2}+(3\sqrt{3})^{2}}$=6,
∵BC=2,
∴AC=4,
过B作BE⊥OA于E,CF⊥OA与F,
∴CF∥BE,
∴△ACF∽△ABE,
∴$\frac{AC}{AB}$=$\frac{AF}{AE}$=$\frac{CF}{BE}$,
∴AF=2,CF=2$\sqrt{3}$,
∴OF=4,
∴OC=$\sqrt{C{F}^{2}+O{F}^{2}}$=2$\sqrt{7}$,
∵BD=OC,
∴BD=2$\sqrt{7}$,
设D(x,0),
∴BD=$\sqrt{(3-x)^{2}+(3\sqrt{3})^{2}}$=2$\sqrt{7}$,
∴x1=2,x2=4,
∴D(2,0)或(4,0).
故答案为:D(2,0)或(4,0).
点评 本题考查了抛物线与x轴的交点,相似三角形的判定和性质,勾股定理,待定系数法求函数的解析式,正确的作出辅助线是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -3 | B. | |-2| | C. | (-3)2 | D. | -22 |
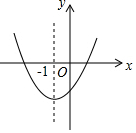 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴方程为x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0,则正确的结论是( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴方程为x=-1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a-b+c<0,则正确的结论是( )| A. | ①②③④ | B. | ②④⑤ | C. | ①④⑤ | D. | ②③④ |
 如图,点E是正方形ABCD的边BC延长线上的一点,AC=CE,AE交CD于点F,则∠AFD的度数是67.5°.
如图,点E是正方形ABCD的边BC延长线上的一点,AC=CE,AE交CD于点F,则∠AFD的度数是67.5°.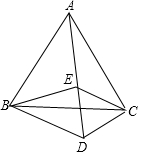 如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.
如图,△ABC和△CDE都是等边三角形,点A、E、D在同一条直线上,且∠EBD=62°,求∠AEB的度数.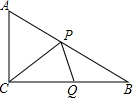 如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,
如图,Rt△ABC中,∠ACB=90°,CA=3cm,CB=4cm,设点P、Q为AB、CB上动点,它们分别从A、C同时出发向B点匀速移动,移动速度都为1cm/秒,移动时间为t秒(0≤t≤4),在整个移动过程中,