题目内容
17.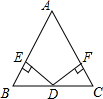 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,求证:△BDE≌△CDF.
如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,求证:△BDE≌△CDF.
分析 根据等腰三角形的性质得到∠B=∠C,利用中点的定义得到BD=CD,进而利用AAS证明△BDE≌△CDF.
解答 证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED和△CFD中,
∵$\left\{\begin{array}{l}{∠B=∠C}\\{∠BED=∠CFD=90°}\\{BD=CD}\end{array}\right.$,
∴△BDE≌△CDF.
点评 本题主要考查了全等三角形的判定以及等腰三角形的性质,解题的关键是掌握AAS证明两个三角形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.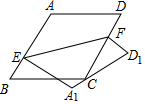 如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )
如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )
 如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )
如图,折叠菱形纸片ABCD,使得AD的对应边A1D1过点C,EF为折痕,若∠B=60°,当A1E⊥AB时,$\frac{BE}{AE}$的值等于( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}-1}{6}$ | C. | $\frac{\sqrt{3}+1}{8}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
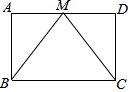 已知:如图,M是矩形ABCD的边AD的中点,求证:MB=MC.
已知:如图,M是矩形ABCD的边AD的中点,求证:MB=MC. 在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠AED+∠AFD=180°,求证:DE=DF.
在△ABC中,AD是∠BAC的平分线,E、F分别为AB、AC上的点,且∠AED+∠AFD=180°,求证:DE=DF. 已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.
已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B、C两点.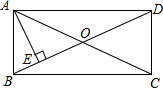 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$. 如图,正方形ABCD的边长为2cm,分别以A为原点,AB,AD边所在的直线为坐标轴建立平面直角坐标系后,将正方形ABCD以点B为旋转中心,沿着x轴的正方向顺时针旋转90°称为第一次振动,再以点C为旋转中心沿着x轴的正方向顺时针旋转90°称为第2次滚动…,以此类推,将正方形ABCD做无滑动地滚动下去.则第2017次滚动时点A的对应点的运动路径长是(504.5+252$\sqrt{2}$)πcm.
如图,正方形ABCD的边长为2cm,分别以A为原点,AB,AD边所在的直线为坐标轴建立平面直角坐标系后,将正方形ABCD以点B为旋转中心,沿着x轴的正方向顺时针旋转90°称为第一次振动,再以点C为旋转中心沿着x轴的正方向顺时针旋转90°称为第2次滚动…,以此类推,将正方形ABCD做无滑动地滚动下去.则第2017次滚动时点A的对应点的运动路径长是(504.5+252$\sqrt{2}$)πcm.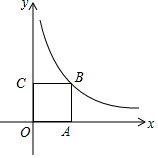 如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.
如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.